定義
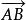 自由向量
自由向量 自由向量
自由向量在物理學中講到的力、速度等都是向量,為了研究這一類向量及其運算性質,數學上將這一類向量進一步抽象為 自由向量:只考慮具有大小和方向的量,而不考慮別的因素,並用帶箭頭的線段表示向量,線段的長度表示 向量的大小,箭頭的指向為 向量的正向。如圖1所示的向量便記為 ,也記為 ,因為是自由向量,故向量的起點可以在空間的任何位置,只要大小相等,方向一致就表示同一個向量。
 圖1
圖1向量相等
 自由向量
自由向量 自由向量
自由向量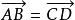 自由向量
自由向量在自由向量的意義下,如圖2,如果向量 與 大小相等,互相平行且指向一致,就說它們 相等,記為 。
兩向量共線
 自由向量
自由向量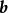 自由向量
自由向量 自由向量
自由向量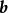 自由向量
自由向量 自由向量
自由向量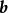 自由向量
自由向量 自由向量
自由向量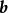 自由向量
自由向量 自由向量
自由向量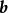 自由向量
自由向量兩平行向量 與 ,可以平移至同一條與它們平行的直線上,故稱此二向量 與 共線,也稱向量 與 線性相關,否則,即 不平行於 時,稱與 線性無關。
 自由向量
自由向量 自由向量
自由向量 自由向量
自由向量 自由向量
自由向量 自由向量
自由向量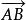 自由向量
自由向量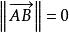 自由向量
自由向量向量 的大小也叫 的 長度、 模或 範數,記為||||,它是個非負實數,當||||=0時,稱 為零向量,記為 0,用帶箭頭的線段表示向量(如 )時,意味著起點A與終點B相重合,即 零向量是一個 點 向量,而當A與B重合時,向量的方向便無意義,所以零向量是唯一的一個方向無意義的向量,這樣,我們又可以說 零向量與任意的向量共線,或說 零向量與任意的向量線性相關。
當我們引入向量的概念後,要注意區別數量與向量。
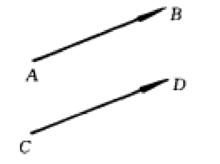 圖2
圖2向量的線性運算
向量的加法、減法以及向量與數的乘法都稱為向量的 線性運算。
向量的加法與減法
 自由向量
自由向量 自由向量
自由向量 自由向量
自由向量 自由向量
自由向量 自由向量
自由向量設有兩向量與 b,如果把 b的起點平移至的終點,那么由的起點到 b的終點的向量稱為向量與 b的和,記為+ b,通常稱為向量相加的 三角形法則,如圖3所示。
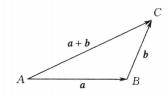 圖3
圖3 自由向量
自由向量 自由向量
自由向量 自由向量
自由向量 自由向量
自由向量將兩個不平行向量, b的起點平移至同一點,以與 b為鄰邊作平行四邊形,則從起點到平行四邊形的對角頂點的向量就是向量與 b的和+ b .通常稱為向量相加的 平行 四邊形法則,如圖4所示。
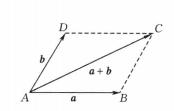 圖4
圖4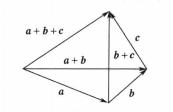 圖5
圖5向量的加法滿足交換律與結合律,如圖4、圖5所示。
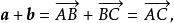 自由向量
自由向量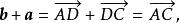 自由向量
自由向量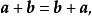 自由向量
自由向量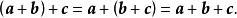 自由向量
自由向量多個向量相加,可以將前一向量的終點作為次一向量的起點,依次作出各向量,最後以第一個向量的起點為起點、最後一個向量的終點為終點作一向量,該向量即為所求的和,如圖6所示,有
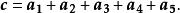 自由向量
自由向量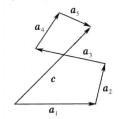 圖6
圖6 自由向量
自由向量 自由向量
自由向量 自由向量
自由向量 自由向量
自由向量設有兩個向量與 b,若有另一個向量,它與相加後等於 b,則這個向量稱為向量 b與的差,記為 b-,如圖7所示。
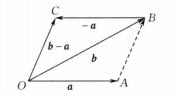 圖7
圖7 自由向量
自由向量 自由向量
自由向量 自由向量
自由向量 自由向量
自由向量 自由向量
自由向量 自由向量
自由向量這樣,對於每一個向量,有 0與的差; 0-是與大小相等而方向相反的一個向量,記為-,稱為的負向量,這樣,就有
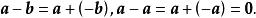 自由向量
自由向量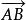 自由向量
自由向量任給向量及點 O,顯然有
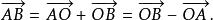 自由向量
自由向量不難根據三角形兩邊之和大於第三邊的原理,得出
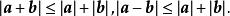 自由向量
自由向量向量與數的乘法
 自由向量
自由向量 自由向量
自由向量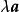 自由向量
自由向量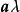 自由向量
自由向量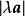 自由向量
自由向量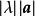 自由向量
自由向量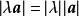 自由向量
自由向量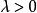 自由向量
自由向量 自由向量
自由向量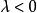 自由向量
自由向量 自由向量
自由向量 自由向量
自由向量一個向量與數的乘積,記為或,該向量的模等於,即,它的方向當時與相同,當時與相反,同時,0= 0。
不難證明,向量與數的乘法滿足下列運算規律:
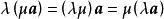 自由向量
自由向量(1)結合律;
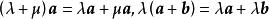 自由向量
自由向量(2)分配律。
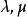 自由向量
自由向量其中都是實常數。
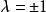 自由向量
自由向量特別地,當時,有
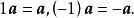 自由向量
自由向量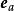 自由向量
自由向量 自由向量
自由向量設表示與非零向量同方向的單位向量,則根據向量與數的乘法,顯然有
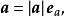 自由向量
自由向量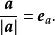 自由向量
自由向量這表明一個非零向量與它的模的比值是一個與原向量同方向的單位向量。