定義
 相反向量
相反向量 相反向量
相反向量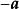 相反向量
相反向量 相反向量
相反向量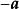 相反向量
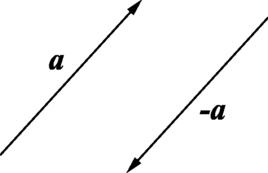
相反向量與向量長度相等,方向相反的向量,叫作向量的相反向量,記作,由於方向反轉兩次仍回到原來的方向,因此和互為 相反向量。
規定,零向量的相反向量仍是零向量。
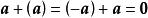 相反向量
相反向量任一向量與其相反向量的和是零向量,即。
 相反向量
相反向量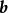 相反向量
相反向量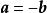 相反向量
相反向量向量與向量相反,記作。
 圖1 相對的兩個長度相等的向量是相反向量
圖1 相對的兩個長度相等的向量是相反向量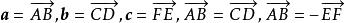 相反向量
相反向量如圖2,有。
 圖2
圖2相關概念
向量
向量:既有大小又有方向的量叫做向量。如物理學中的位移、力、速度、加速度等物理量都是向量 。
向量的表示方法:
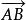 相反向量
相反向量(1) 幾何表示法:用有向線段表示,如下圖向量。
 圖3
圖3 相反向量
相反向量 相反向量
相反向量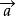 相反向量
相反向量(2) 字母表示法:用一個小寫字母表示,如(註:印刷用黑體,手寫用)。
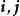 相反向量
相反向量 相反向量
相反向量 相反向量
相反向量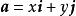 相反向量
相反向量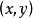 相反向量
相反向量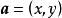 相反向量
相反向量(3) 坐標表示法:在直角坐標系中,分別取與x軸,y軸方向相同的兩個單位向量作為基底,則對任一向量,有且只有一對實數,使,就把叫做向量的(直角)坐標,記作。
向量的模
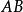 相反向量
相反向量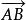 相反向量
相反向量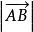 相反向量
相反向量向量的模:線段的長度也叫做向量的長度,記作。向量的長度也稱為向量的模。
向量的三要素:起點、方向、長度 。
零向量
零向量:長度為零的向量叫做零向量,記為 0。
單位向量
單位向量:長度等於一個單位長度的向量叫做單位向量。
自由向量
自由向量:一個向量只要不改變它的大小和方向,它的起點和終點可以任意平行移動的向量,叫做自由向量。
平行向量
 相反向量
相反向量 相反向量
相反向量平行向量:方向相同或相反的非零向量叫做平行向量(也稱為 共線向量)。向量與向量 b平行,記作// b。如下圖所示。
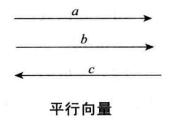 圖4
圖4相等向量
相等向量:長度相等且方向相同的向量叫做相等向量。
 相反向量
相反向量 相反向量
相反向量向量與向量 b相等,記作= b。
註:零向量與零向量相等;任意兩個相等的非零向量,都可以用一條有向線段表示,並且與有向線段的起點無關 。