簡介
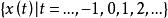 平穩時間序列
平穩時間序列記 為一時間序列,其中時刻 t 可取遍正負整數和零值。這不僅符合多數真實情況,而且便於理論分析。
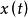 平穩時間序列
平穩時間序列 平穩時間序列
平穩時間序列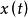 平穩時間序列
平穩時間序列 平穩時間序列
平穩時間序列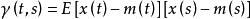 平穩時間序列
平穩時間序列此時記的均值為,顯然它是隨 t 而變化的函式,類似地,與 但協方差,及它們的相關係數
 平穩時間序列
平穩時間序列自然是 t 和 s 的二元函式。
 平穩時間序列
平穩時間序列 平穩時間序列
平穩時間序列 平穩時間序列
平穩時間序列 平穩時間序列
平穩時間序列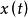 平穩時間序列
平穩時間序列 平穩時間序列
平穩時間序列 平穩時間序列
平穩時間序列如果其均值 為常數值,和 只依賴於之值,則稱此序列為平穩時間序列。此時與 的相關係數與 t 無關,所以可記。
套用
平穩時間序列是時間序列分析中最重要的特殊類型。到目前為止,時間序列分析基本上是以平穩時間序列為基礎的,對於非平穩時間序列的統計分析,其方法和理論都很有局限性。
相關概念
時間序列
時間序列(或稱動態數列)是指將同一統計指標的數值按其發生的時間先後順序排列而成的數列。時間序列分析的主要目的是根據已有的歷史數據對未來進行預測。
構成要素:長期趨勢,季節變動,循環變動,不規則變動。
長期趨勢(T)現象在較長時期內受某種根本性因素作用而形成的總的變動趨勢。
季節變動(S)現象在一年內隨著季節的變化而發生的有規律的周期性變動。
循環變動(C)現象以若干年為周期所呈現出的波浪起伏形態的有規律的變動。
不規則變動(I)是一種無規律可循的變動,包括嚴格的隨機變動和不規則的突發性影響很大的變動兩種類型。
時間序列分析
時間序列分析是根據系統觀測得到的時間序列數據,通過曲線擬合和參數估計來建立數學模型的理論和方法。它一般採用曲線擬合和參數估計方法(如非線性最小二乘法)進行。時間序列分析常用在國民經濟巨觀控制、區域綜合發展規劃、企業經營管理、市場潛量預測、氣象預報、水文預報、地震前兆預報、農作物病蟲災害預報、環境污染控制、生態平衡、天文學和海洋學等方面。
補充說明
AR模型
時間序列
自回歸模型
ARMA模型

