定義
平均數不等式，或稱 平均值不等式、 均值不等式，是數學上的一組不等式，也是基本不等式的推廣。它是說：
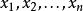平均數不等式如果 是正數，則
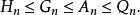平均數不等式其中：
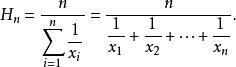平均數不等式
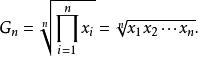平均數不等式
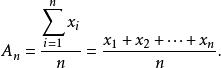平均數不等式
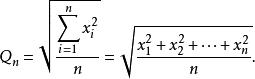平均數不等式
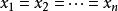平均數不等式若且唯若 ，等號成立。即對這些正數：調和平均數≤幾何平均數≤算術平均數≤平方平均數（方均根）簡記為：“ 調幾算方”。
證明方法
關於均值不等式的證明方法有很多，數學歸納法（第一數學歸納法或反向歸納法）、拉格朗日乘數法、琴生不等式法、排序不等式法、柯西不等式法等等，都可以證明均值不等式，在這裡簡要介紹數學歸納法證明n維形式的均值不等式的方法：
用數學歸納法證明，需要一個輔助結論。
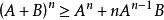平均數不等式引理：設A≥0，B≥0，則 ，且僅當B=0時取等號。
引理的正確性較明顯，條件A≥0，B≥0可以弱化為A≥0，A+B≥0，可以用數學歸納法證明。
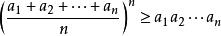平均數不等式
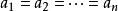平均數不等式原題等價於： ， 若且唯若 時取等號。
當n=2時易證；
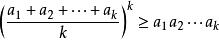平均數不等式
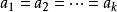平均數不等式假設當n=k時命題成立，即 ， 若且唯若 時取等號。
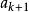平均數不等式
平均數不等式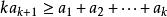
平均數不等式那么當n=k+1時，不妨設 是 中最大者，則 。
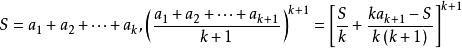平均數不等式設，根據引理
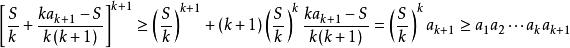平均數不等式
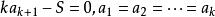平均數不等式
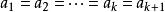平均數不等式，若且唯若時，即時取等號。
利用琴生不等式法也可以很簡單地證明均值不等式，同時還有柯西歸納法等方法。
參見
•算術-幾何平均值不等式
•冪平均不等式
