介紹
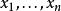算術-幾何平均值不等式
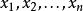算術-幾何平均值不等式
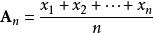算術-幾何平均值不等式
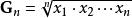算術-幾何平均值不等式算術-幾何平均值不等式，簡稱 算幾不等式，是一個常見而基本的不等式，表現了算術平均數和幾何平均數之間恆定的不等關係。設為n個正實數，它們的 算術平均數是，它們的 幾何平均數是。算術-幾何平均值不等式表明，對任意的正實數，總有：
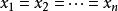算術-幾何平均值不等式
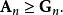算術-幾何平均值不等式等號成立若且唯若。
算術-幾何平均值不等式僅適用於正實數，是對數函式之凹性的體現，在數學、自然科學、工程科學以及經濟學等其它學科都有套用。
算術-幾何平均值不等式有時被稱為 平均值不等式（或 均值不等式），其實後者是一組更廣泛的不等式。
證明
使用常規數學歸納法的證明則有喬治·克里斯托（George Chrystal）在其著作《代數論》（ algebra）的第二卷中給出的：
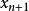算術-幾何平均值不等式
算術-幾何平均值不等式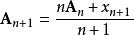
算術-幾何平均值不等式
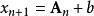算術-幾何平均值不等式
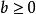算術-幾何平均值不等式
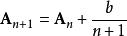算術-幾何平均值不等式由對稱性不妨設 是 中最大的，由於，設，則，並且有。
根據二項式定理，
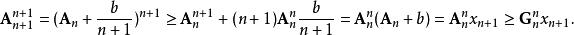算術-幾何平均值不等式
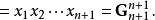算術-幾何平均值不等式於是完成了從n到n+1的證明。
例子
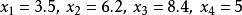算術-幾何平均值不等式在n=4 的情況，設:， 那么
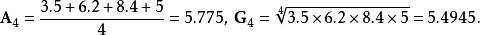算術-幾何平均值不等式
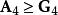算術-幾何平均值不等式可見。
推廣
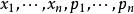算術-幾何平均值不等式
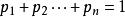算術-幾何平均值不等式不僅“均勻”的算術平均數和幾何平均數之間有不等式，加權的算術平均數和幾何平均數之間也有不等式。設為正實數，並且，那么：
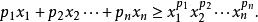算術-幾何平均值不等式加權算術-幾何平均不等式可以由琴生不等式得到。
參見
•平均數不等式
•算術平均數
•幾何平均數
•冪平均不等式
•楊氏不等式
