形狀對稱變換
1、正三角形在下面六個平面剛體運動中保持不變:
(1)恆等變換,記作I。
(2)關於對稱軸r1所在直線的反射,記作r1。
(3)關於對稱軸r2所在直線的反射,記作r2。
(4)關於對稱軸r3所在直線的反射,記作r3。
(5)以重心O為中心轉120° 的旋轉,記作ρ1。
(6)以重心O為中心轉240° 的旋轉,記作ρ2。
正三角形的六個對稱變換組成的集合記作D3,即D3={I,r1,r2,r3,ρ1,ρ2}。
2、正四邊形在下面八個平面剛體運動中保持不變:
(1)恆等變換,記作I。
(2)關於對稱軸r1所在直線的反射 ,記作r1。
(3)關於對稱軸r2所在直線的反射,記作r2。
(4)關於對稱軸r3所在直線的反射,記作r3。
(5)關於對稱軸r4所在直線的反射,記作r4。
(6)以重心O為中心轉90° 的旋轉,記作ρ1。
(7)以重心O為中心轉180° 的旋轉,記作ρ2。
(8)以重心O為中心轉270° 的旋轉,記作ρ3。
正四邊形的八個對稱變換組成的集合記作D4,即D4={I,r1,r2,r3,r4,ρ1,ρ2,ρ3}。
合成
一個平面圖形的兩個對稱變換a與b的合成(先做變換a,再做變換b)仍然是這個平面圖形的 對稱變換,記作b·a 。
性質
1、對於任意對稱變換a與恆等變換I,都有a·I=I·a。
2、一般地,平面圖形的對稱變換不滿足交換律(除恆等變換外)。
3、平面圖形的對稱變換滿足結合律。
分類
對稱變換主要有 :
1、 y= f(- x) 與 y= f( x) 的圖象關於 y軸對稱;
若 f(- x)= f( x),則函式自身的圖象關於 y軸對稱。
2、 y=- f( x) 與 y= f( x) 的圖象關於 x軸對稱。
3、 y=- f(- x) 與 y= f( x) 的圖象關於原點對稱;
若 f(- x)=- f( x),則函式自身的圖象關於原點對稱。
4、 y= f( x) 與 y= f( x) 的圖象關於直線 y= x對稱。
5、 y=- f(- x) 與 y= f( x) 的圖象關於直線 y=- x對稱。
6、 y= f(2 a- x) 與 y= f( x) 的圖象關於直線 x= a對稱;
若 f( x)= f(2 a- x)(或 f( a+ x)= f( a- x)),則函式自身的圖象關於直線 x= a對稱。
7、 y=2 b- f( x) 與 y= f( x) 的圖象關於直線 y= b對稱。
8、 y=2 b- f(2 a- x) 與 y= f( x) 的圖象關於點( a, b)對稱。
例1、設函式 y= f( x)的定義域是 R,且 f( x-1)= f(1- x),那么 f( x)的圖象有對稱軸( )。
A.直線 x=0 B.直線 x=1
C.直線 y=0 D.直線 y=1
【解析】設 x-1= t,則 f( t)= f(- t),函式為偶函式,關於 y軸對稱。故答案選D。
例2、已知函式 f( x)定義域為 R,則下列命題中
① y= f( x)為偶函式,則 y= f( x+2)的圖象關於 y軸對稱.
② y= f( x+2)為偶函式,則 y= f( x)關於直線 x=2對稱.
③若 f( x-2)= f(2- x),則 y= f( x)關於直線 x=2對稱.
④ y= f( x-2)和 y= f(2- x)的圖象關於 x=2對稱.
其中正確命題序號有_____(填上所有正確命題序號).
【解析】 ① y= f( x)是偶函式,而 f( x+2)是將 f( x)的圖象向左平移2個單位得到的,則對稱軸左移2個單位為 x=-2,所以 f( x+2)圖象關於直線 x=-2對稱。
② y= f( x+2)為偶函式,則 f( x+2)= f(2- x),所以 y= f( x)圖象關於直線 x=2對稱。
③令 x-2= t ,則2- x=- t,得 f( t)= f(- t), y= f( x)的圖象關於 y軸對稱。
④ f( x)與 f(- x)的圖象關於 y軸對稱,將 f( x)與 f(- x)的圖象分別向右平移2個單位,分別得到 f( x-2)與 f(2- x)的圖象,對稱軸右移2個單位為直線 x=2.。
【答案】 ②④
逆變換
1、若兩個對稱變換a、b滿足a·b=b·a=I,那么b(或a)叫做a(或b)的 逆變換,記作
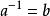 對稱變換
對稱變換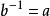 對稱變換
對稱變換或
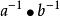 對稱變換
對稱變換2、b·a的逆變換是。
多項式
1、如果一個多項式F經過字母的替換仍與原來的多項式相等,那么就說F具有 對稱性,上述字母的替換叫做 多項式的對稱變換 。
2、設一個多項式的下標組成的集合為{1,2,3,…,n},σ是n元對稱群S中的一個置換,如果對多項式的下標進行置換σ後仍與原來的多項式相等,那么置換σ就叫做 多項式的對稱變換。
3、如果一個n次多項式的對稱變換是S中的全部變換,這樣的多項式叫做 對稱多項式。

