孫子剩餘定理
正文
中國南北朝時期（5～6世紀）著名的著作《孫子算經》中“物不知數”問題所闡述的定理。物不知數問題的原題是：“今有物，不知其數，三三數之剩二，五五數之剩三，七七數之剩二，問物幾何？”這屬於數論的一次同餘方程組問題。用現代數學符號可表為求下列同餘方程的整數解：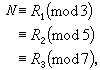
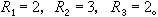
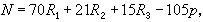
上述問題和解法，可直接推廣為定理：設α1,α2,…,αn兩兩互素，
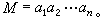則 
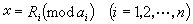, (1)
,
。
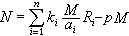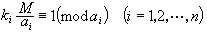《孫子算經》沒有給出求kj的具體算法。宋代秦九韶在《數書九章》中第一次詳細地、完整地闡述了求解一次同餘方程組的算法，他稱做“大衍總數術”，其中包括求kj的一種機械化算法──大衍求一術。
秦九韶稱αj為“定數”，kj為“乘率”,由
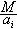中屢減αj所得的餘數Gj(<αj)為“奇數”。“大衍求一術云：置奇右上，定居右下,立天元一於左上(圖1
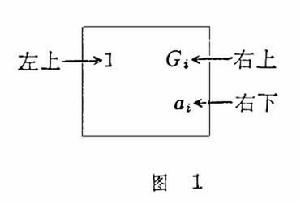)。先以右上除右下，所得商數與左上一相生(即相乘)入左下。然後乃以右行上下以少除多，遞互除之，所得商數隨即遞互累乘歸左行上下，須使右上末後奇一而止。乃驗左上所得，以為乘率。”秦九韶在例題中曾以Gj=3,αj=4為例，列出求kj的算草布式：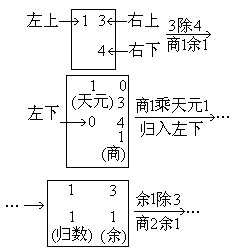 
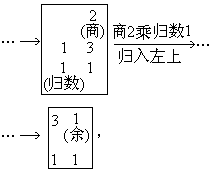
秦九韶還在歷史上首次提出了當 α1,α2,…,αn並非兩兩互素時, 求解(1)的方法。他設計了“兩兩連環求等,約奇弗約偶”，"復乘求定"等算法,先約去諸模數α1,α2,…,αn中包含的多餘的因子,得到新的一組
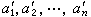,使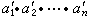 
恰為 α1,α2,…,αn的最低公倍數。再對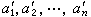,中的因子重新歸併，得到
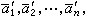使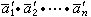
仍為α1,α2,…,αn的最低公倍數，且它們兩兩互素。這樣便將問題化約為模數兩兩互素的情形。秦九韶尚未提及當α1,α2,…,αn並非兩兩互素時，方程(1)可解的條件。但從他所舉八道例題中有七道的模數滿足可解條件這一事實分析，許多人認為秦九韶已知道該條件。