秦九韶(約1202~約1261)
正文
中國南宋數學家。字道古,普州安岳(今四川省安岳縣)人。活動在南宋末年,青少年飽經戰爭憂患,成年後被迫離開四川,在湖北、安微、江蘇、浙江等地做官,晚年受賈似道打擊,貶於梅州,“在梅治政不輟”,死於任所。秦九韶自稱年輕時在杭州“訪習於太史,又嘗從隱君子受數學”。他知識淵博,當時人們稱他“性極機巧,星象、音律、算術以至營造等事無不精究”。秦九韶對數學的看法是矛盾的,他混淆了數學科學和術數的界限,把“通神明,順性命”看成大者,把“經世務,類萬物”看成小者,並進而認為河圖、洛書揭開了數學的奧秘,說“數與道非二本”,表示要把他的數學成就“進之於道”。然而,數學研究的實踐又使他承認他對通神明、順性命的認識非常膚淺,承認“數術之傳,以實為體”,從而把主要精力用於“經世務”,從社會實踐和需要抽象數學問題。
秦九韶論述了數學在計算日月五星位置、改革曆法、測量雨雪、度量田域、測高求遠、軍事部署、財政管理、建築工程以及商業貿易等中的巨大作用,認為不進行計算會造成“財蠹力傷”的後果,而計算不準確,“差之毫厘,謬乃千百”,於私於公都沒有好處。因此他注意搜求生產、生活、交換以及戰爭中的數學問題,“設為問答以擬於用”,終於在1247年寫成傑作《數書九章》。
《數書九章》,南宋時稱為《數學大略》或《數術大略》,明朝時又稱為《數學九章》。全書共18卷,81題,分為九大類。第一,大衍類,集中闡述了他的重要成就──大衍求一術,即一次同餘式組解法(見孫子剩餘定理)。秦九韶指出"大衍之法不載九章",歷算家制定曆法時雖然用到這種方法,但誤以為是線性方程組問題。他總結了歷算家計算上元積年的方法,在《孫子算經》“物不知數”題的基礎上,系統地提出了一次同餘式組解法。並針對不同的情況,提出了不同的程式。他還把這種理論用於解決商功、利息、粟米、建築等問題。第二,天時類,是有關曆法推算及降雨降雪量的測量。第三,田域類,是面積問題。第四,測望類,是勾股重差問題。第五,賦役類,是均輸及租稅問題。第六,錢穀類,是糧谷轉運和倉庫容積問題。第七,建設類,是建築工程問題。第八,軍旅類,是營盤布置及軍需供應問題。第九,市易類,是交易及利息問題。後八類問題都是按套用分類,其中最重要的成就是正負開方術,今稱秦九韶程式,即以增乘開方法為主導求高次方程正根的方法。他用這種方法解決了21個問題共26個方程,其中二次方程20個,三次方程1個,四次方程4個,還用勾股差率列出了一個十次方程。在這裡,秦九韶把賈憲開創的增乘開方法發展到十分完備的地步。在開方中,他發展了劉徽開方不盡求微數的思想,在世界數學史上第一次用十進小數表示無理根的近似值。其次是在卷五“三斜求積”題中提出了已知三角形三邊ɑ,b,с,求面積的公式
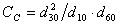
與以往的數學著作比較,《數書九章》中的問題更加複雜,如卷十三“計定築城”題已知條件達88個,卷九“復邑修賦”題的答案有180個。因此,《數書九章》也更加翔實地反映了南宋的社會經濟情況,保存了非常有價值的歷史資料。
《數書九章》也有不容忽視的缺點。如第一題將大衍求一術附會《周易》"大衍之數五十,其用四十有九",不足為訓。還有一些問題,甚至某些不難的勾股測量問題,題設和演算都出現錯誤。
《數書九章》問世後,當時流傳不廣,明《永樂大典》鈔錄此書,稱為《數學九章》。清四庫館本《數學九章》轉錄自《永樂大典》,並加校訂。後李銳又略加校注。明萬曆年間趙琦美有另一鈔本《數書九章》。清沈欽裴、宋景昌以趙本為主,參考各家校本,重加校訂,1842年收入上海郁松年所刻《宜稼堂叢書》。此後,又有《古今算學叢書》本,商務印書館《叢書集成》本均據此翻印,成為最流行的版本。
