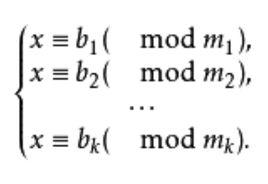基本概念
所謂一次同餘方程組，是指k(k∈Z ，k>1)個一次同餘方程構成的方程組
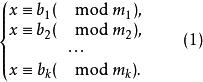一次同餘方程組或記為
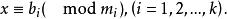一次同餘方程組
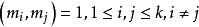一次同餘方程組同餘方程中的模 。當k=2時是最簡單的一次同餘方程組，即
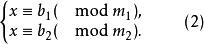一次同餘方程組在同餘方程組(2)中，設(m，m)=d，M=mm。若d∤(b-b)，則同餘方程組(2)無解。若d|(b-b)，則方程(2)對模M有解。設解為x≡x(mod M)，則x=b+mt，t為mt≡b-b(mod m)的任一解，關於一般同餘方程組(1)的解法參見下文 。
一次同餘方程組的解法
一次同餘方程組的方法及解的充要條件由以下兩個定理給出。
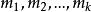一次同餘方程組定理1（孫子定理）設 是k個兩兩互素的正整數，令
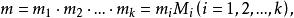一次同餘方程組則同餘方程組(1)有唯一解：
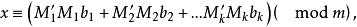一次同餘方程組
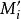一次同餘方程組
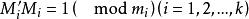一次同餘方程組其中 是由 得出的。
定理2 一次同餘式
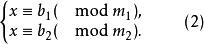一次同餘方程組
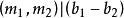一次同餘方程組
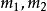一次同餘方程組可解的充要條件是 ，且當(2)可解時，對模 有唯一解 。
上面的孫子定理其實是《孫子算經》卷中記載的“今有物不知其數”一題的解法的推廣，這道題是：
“今有物不知其數，三三數之剩二，五五數之剩三，七七數之剩二，問物幾何？”答曰二十三。
術日：三三數之剩二，置一百四十；五五數之剩三，置六十三；七七數之剩二，置三十；並之，得二百三十三，以二百一十減之，即得二十三。
術中說：三三數之剩一，則置七十，三三數之剩二，就置一百四
十；五五數之剩一，則置二十一，五五數之剩三，則置六十三；七七數之剩一，則置十五，七七數之剩二，就置三十。若在一百六十五以上，就以一百零五減之，或多則退二百一十。
宋朝周密《志雅堂雜鈔》卷中記載有鬼谷算，又叫隔牆算，將此題的解法用一句詩隱括為：
“三歲孩兒七十稀，五留廿一事由奇。七度上元重相會，寒食清明便可知。”
明朝程大位《算法統宗》卷中記載孫子歌，隱括此題解法，更是膾炙人口，孫子歌曰（又名韓信點兵）：
“三人同行七十稀，五樹梅花廿一枝。七子團圓正月半，除百零五便得知。”
設x為所求，依題意列式：
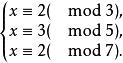一次同餘方程組孫子歌中所隱含的解法，與孫子算經術日中所說的是一致的，現列表解釋如下
| 除數 | 餘數 | 最低公倍 | 衍數 | 乘率 | 各總 | 答數 | 最小答數 | ||
| 3 | 2 | 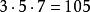 一次同餘方程組 | 5·7 | 2 | 70·2 | 140+63+30=233 | 233=210=23 | ||
| 5 | 3 | 7·3 | 1 | 21·3 | |||||
| 7 | 2 | 3·5 | 1 | 15·2 | |||||
現在我們用孫子定理來解“今有物不知其數”這一題。
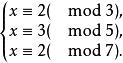一次同餘方程組按孫子定理，先解同餘方程
35x≡1( mod 3),21x≡1( mod 5),15x≡1( mod7)，
分別得其解
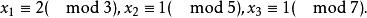一次同餘方程組所以
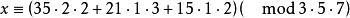一次同餘方程組
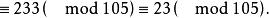一次同餘方程組變數x的通解式為
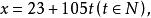一次同餘方程組且23為最小正整數 。
例題解析
例1解同餘方程組：
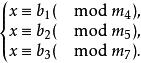一次同餘方程組解 由4·5·7=4·35=5·28=7·20得出公式中的
m₁=4，M₁= 35，
m₂ =5，M₂= 28，
m₃=7，M₃= 20，
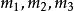一次同餘方程組
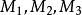一次同餘方程組
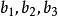一次同餘方程組其中 依次為同餘方程的模， 依次為它的衍數， 依次為各個同餘方程的常數項。按孫子定理，先來解同餘方程
由35x≡1(mod 4)，解得x≡3( mod 4)，
由28x≡1( mod 5)，解得x≡2( mod 5)，
由20x≡1( mod 7)，解得x≡6( mod 7)，
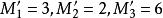一次同餘方程組由此得乘率： ，所以
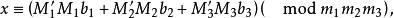一次同餘方程組
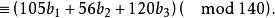一次同餘方程組