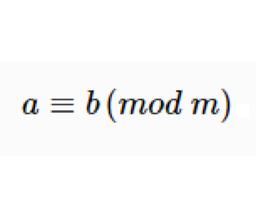基本概念
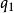 同餘式
同餘式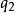 同餘式
同餘式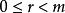 同餘式
同餘式一個整數a被m除時,得到商 和唯一的一個餘數r,另一個整數b也被m除時,得到商 ,得到的唯一餘數r也是,即(其中 )
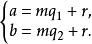 同餘式
同餘式那么我們說a與b對於模m,有同一個餘數r,寫成
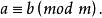 同餘式
同餘式可以簡略地讀作:對於模m,a和b同餘,其中mod是英文模module的縮寫。
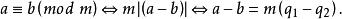 同餘式
同餘式同餘式的性質
(1)同餘式可以逐項相加。
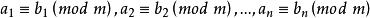 同餘式
同餘式若 ,則
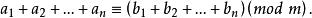 同餘式
同餘式(2)同餘式一邊的數可以移到另一邊,只要改變符號就可以了。
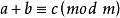 同餘式
同餘式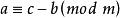 同餘式
同餘式若 ,則。
(3)同餘式的每一邊都可以增加或減去模的任意倍數。
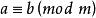 同餘式
同餘式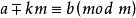 同餘式
同餘式若,則。
(4)同餘式可以逐項相乘。
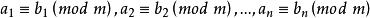 同餘式
同餘式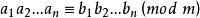 同餘式
同餘式若,則。
(5)我們可以將性質(1)(4)推廣成以下的情形。
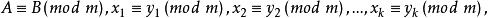 同餘式
同餘式①若則
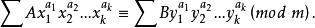 同餘式
同餘式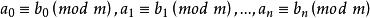 同餘式
同餘式②若,則
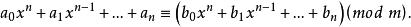 同餘式
同餘式(6)同餘式兩邊的數如有公約數,此公約數又和模互素,那么就可以把兩邊的數除以這個公約數。
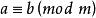 同餘式
同餘式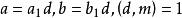 同餘式
同餘式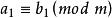 同餘式
同餘式若,且,則。
(7)同餘式兩邊的數和模可以同時乘上一個整數。
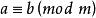 同餘式
同餘式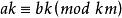 同餘式
同餘式若,則。
(8)同餘式兩邊的數和模可以同時被它們任一公約數除。
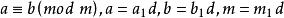 同餘式
同餘式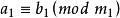 同餘式
同餘式若,則。
(9)如果同餘式對於模m成立,那么它對於m的任意約數相等的模d也成立。
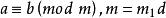 同餘式
同餘式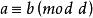 同餘式
同餘式若,則。
(10)如果同餘式一邊上的數和模能被某個數除盡,則同餘式的另一邊的數也能被這個數除盡。
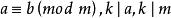 同餘式
同餘式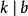 同餘式
同餘式若,則。
(11)同餘式一邊上的數與模的最大公約數,等於另一邊上的數與模的最大公約數。
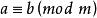 同餘式
同餘式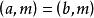 同餘式
同餘式若,則。
孫子剩餘定理
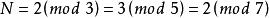 同餘式
同餘式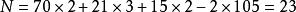 同餘式
同餘式在三國兩晉南北朝時期的數學著作中,《孫子算經》卷下的“物不知數問題”和《張丘建算經》卷下的“百雞問題”,是世界著名的數學問題。《孫子算經》三卷,作者不詳,約成書於公元400年前後,《張丘建算經》三卷,作者張丘建,清河(今河北清河)人,生平不詳,約成書於公元466至485年之間。這兩部著作都被收入唐代《十部算經》,立於學官,並流傳至今。“物不知數問題”亦稱“孫子問題”,大意是:有物不知其數,三個一數餘二,五個一數餘三,七個一數餘二,問該物總數共有多少?這個問題應該求解一次同餘組:,答案是。後來,孫子問題成為廣泛流傳的一種數學遊戲,被稱為“韓信點兵”等,並且還編有一首“孫子歌”:“三人同行七十稀,五樹梅花廿一枝,七子團圓正半月,除百零五便得知”,這首歌訣暗示出問題的解法。但這不是同餘式的一般解法。“孫子問題”與古代曆法中推算上元積年有關,南宋數學家秦九韶創造“大衍求一術”,完滿地解決了這一問題。他所得到的一次同餘組解法公式,現被稱為“孫子剩餘定理”。
“百雞問題”的大意是:公雞1隻,值錢5文;母雞1隻,值錢3文;小雞3隻,值錢1文。今有100文錢買雞100隻,問可買公雞、母雞和小雞各多少只?此題有三個未知數,僅能列出兩個方程,屬於不定方程問題。《張丘建算經》給出三組答案,並有一段說明文字。但是由於其中沒有具體解法,因而引起種種猜測。對於中國古代如何解不定方程,至今眾說紛紜,尚無定論,不定方程問題最早見於《九章算術》方程章的“五家共井”題,但術文簡略,暗含限制條件,沒有一般解法。北周甄鸞《數術記遺》也收錄了百雞問題,但數據與《張丘建算經》有所不同。該題應有兩組答案,但他僅給出一組,並說明這類問題“不用算籌,宜以心計”,即採用試算的辦法去解決。南宋楊輝《續古摘奇算法》引述了《辯古根源》(已失傳)中的“百橘問題”,該題應有四組答案,書中僅列出一種,是不完全的。直到19世紀,清代數學家才把這種類型的問題和求一術(一次同餘組問題)聯繫起來,獲得了比較完善的解法。晚於《九章算術》時代的公元3世紀古希臘數學家丟番圖,對不定方程問題進行了深入的研究,取得了非常出色的成果。15世紀中亞數學家阿爾·卡西的“百禽問題”,與“張丘建算經”的“百雞問題”非常類似,很有可能受到中國數學的影響。