外爾斯特拉斯，K.（T.W.）
正文
德國數學家。1815年10月31日生於威斯伐倫州的奧斯滕費爾德,1897年2月19日卒於柏林。1834年他遵照父親的意願入波恩大學學習法律和財政，但他的興趣卻在數學。1838年轉學數學。1842～1856年，先後在幾所中學任教。1854年3月31日獲得柯尼斯堡大學名譽博士學位。1856年10月受聘為柏林大學助理教授，同年成為柏林科學院成員，1864年升為教授。 外爾斯特拉斯的主要貢獻在函式論和分析學方面。他在大學期間閱讀了C.古德爾曼的論文，對橢圓函式論發生很大興趣。在1854年發表的《關於阿貝爾函式理論》的論文中，解決了橢圓積分的逆轉問題，引起數學界的重視。1856年發表的《阿貝爾函式理論》進一步解決了橢圓積分的雅可比逆轉問題。他還建立了橢圓函式新結構的定理，一致收斂的解析函式項級數的和函式的解析性的定理，圓環上解析函式的冪級數展開定理（又稱洛朗定理）等。
他把嚴格的論證引進分析學，建立了實數理論，引進了現在通用的極限的ε-δ 定義，在此基礎上給出了連續函式的嚴格定義和性質，他還構造了一個著名的處處不可微的連續函式：
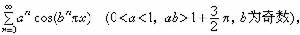
外爾斯特拉斯一生中培養了很多有成就的學生，其中著名的有С.Β.柯瓦列夫斯卡婭、H.A.施瓦茲、I.L.富克斯、（M.）G.米塔－列夫勒等。
1887年外爾斯特拉斯決定將他一生的工作成果整理出版，原計畫出10卷，但生前只出了2卷,他去世後30年，出到第7卷。8～10卷最終未能出版。
