簡介
外爾斯特拉斯定理 外爾斯特拉斯定理波爾查諾－魏爾施特拉斯定理是數學拓撲學與實分析中用以刻劃中的緊集的基本定理，得名於數學家伯納德·波爾查諾與卡爾·魏爾施特拉斯。波爾查諾－魏爾斯特拉斯定理說明，有限維實向量空間中的一個子集E是序列緊緻（每個序列都有收斂子序列）若且唯若E是有界閉集。
歷史
這個定理最早由伯納德·波爾扎諾證明，當他在證明介值定理時，附帶證明了這個定理，但是他的證明已經散佚。卡爾·魏爾施特拉斯獨自發現並證明了這個定理。波爾扎諾-魏爾施特拉斯定理是實分析中的基本定理。
定理
波爾查諾－魏爾斯特拉斯定理可以視為刻畫有限維實向量空間{\displaystyle \mathbb {R} ^{n}}中序列緊緻集合的定理。波爾查諾－魏爾斯特拉斯定理的核心部分可以僅僅使用序列的語言來表示：
定理 1：
外爾斯特拉斯定理
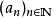外爾斯特拉斯定理任一中的有界序列都至少包含一個收斂的子列。
從這個定理出發，在給定的有界閉集F中任取一個序列，那么這個序列是有界的，從而至少包含一個收斂的子列。而從F的封閉性可知，這個子列作為F的一部分，其收斂的極限必然也在F中。所以可以推知：
推論：
外爾斯特拉斯定理任一中的有界閉集必然序列緊緻。
外爾斯特拉斯定理這個推論給出了中集合序列緊緻的充分條件。另一方面，可以證明序列緊緻的集合必然是有界閉集。這樣就將充分條件推進為充要條件：
定理 2：
外爾斯特拉斯定理 外爾斯特拉斯定理中的一個子集E是序列緊緻的，若且唯若E是有界閉集。由於有限維賦范向量空間都與裝備了歐幾里德範數的同胚，所以以上的定理都可以擴展到任意有限維賦范向量空間。
波爾查諾－魏爾斯特拉斯性質
在有限維度量空間中，波爾查諾－魏爾斯特拉斯說明了序列緊緻的集合就是有界閉集。然而在一般的度量空間中，有界閉集不一定是序列緊緻的。為此，拓撲學中將一般度量空間中的序列緊緻稱為波爾查諾－魏爾斯特拉斯性質。
定義：
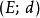外爾斯特拉斯定理 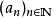外爾斯特拉斯定理設K為度量空間的子集。若K中任一序列都包含一個收斂的子列，其極限也是K中元素，就稱K具有波爾查諾－魏爾斯特拉斯性質。
如果度量空間本身滿足波爾查諾－魏爾斯特拉斯性質，就稱這個度量空間為緊空間。在度量空間中，波爾查諾－魏爾斯特拉斯性質等價于海恩－波萊爾性質：所有K的開覆蓋都有限子覆蓋。
