公式的得出
根據虛功原理計算結構位移的一種方法,因用到虛設的單位載荷而得名,又稱虛功法。該法為英國的J.C.麥克斯韋於1864年、德國的O.莫爾於1874年分別獨立提出,故又稱麥克斯韋-莫爾法。它常用於解決桿、桿繫結構和薄壁結構的問題,對靜定結構和靜不定結構都適用。單位載荷法的原理如下:設結構上作用一個真實的廣義力系(見廣義力)Pi(i=1,2,...,n),並產生變形(圖1),欲求結構上j點在Pi作用下的位移,可在j點處加一虛設的單位載荷Pj=1(圖2)。該虛設載荷的形式必須同所求位移相對應。求線位移時,虛設載荷取單位力;求角位移時,虛設載荷取單位力矩。根據虛功原理,Pj=1在實際力系Pi引起的沿Pj方向的位移△ji上所作的外虛功1·△ji,在數值上等於Pj引起的內力在實際變形過程中所作的內虛功(包括彎曲的內虛功、拉伸或壓縮的內虛功和剪下內虛功),即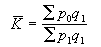 。
。
上式右端有兩組廣義內力:Μ、N、Q分別為實際載荷引起的彎矩、軸力和剪力;嚔、嚻、坴分別為虛設單位載荷引起的彎矩、軸力和剪力;K是與結構截面形狀有關的係數;ds為結構跨度微元;∑為求和號,表示對所有構件求和;E、G分別為材料的楊氏模量和剪下模量(見材料的力學性能);A為構件的截面積;I為構件截面的慣性矩。
關於內力的正負號有如下規定:軸力N、嚻以拉為正;剪力Q、坴以使結構微段順時針轉動為正;彎矩Μ、嚔只規定乘積Μ嚔的正負號,當Μ和嚔使桿件同側纖維受拉時,Μ嚔取正號。
根據各類結構的特點,位移計算公式可作相應簡化:
①桁架
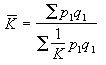
②梁和剛架
③桁架混合結構
④拱
配圖
相關連線
參考書目 S.鐵摩辛柯、J.蓋爾著,胡人禮譯:《材料力學》,科學出版社,北京,1978。(S. Timoshenko and J. Gere, Mechanics of Materials,Van Nostrand Reinhold Co., New York,1972.)范祖堯、郁永熙主編:《結構力學》,機械工業出版社,北京,1980。
龍馭球、包世華主編:《結構力學》,人民教育出版社,北京,1981。