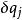 廣義力
廣義力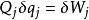 廣義力
廣義力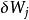 廣義力
廣義力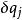 廣義力
廣義力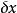 廣義力
廣義力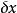 廣義力
廣義力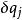 廣義力
廣義力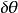 廣義力
廣義力 廣義力
廣義力廣義力是與廣義坐標q對應的力。它的量綱由它與q的虛位移 的乘積構成功的物理量決定。用Q表示廣義力,則 , 為虛功微元。若 為線量 ,且X 為功,則X是作用力。若 為角量 ,且M 為功,則M是力矩。所以廣義的量綱不一定是力的量綱 。
廣義力的定義又可由以下坐標變換式得來:
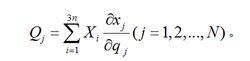 廣義力
廣義力N個自由度的完整系統,有N個廣義力。
對於完整保守系統,存在著勢函式
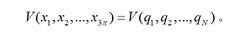 廣義力
廣義力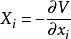 廣義力
廣義力由於 ,代入Q的表達式,得:
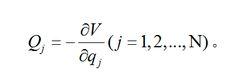 廣義力
廣義力廣義力是與廣義坐標qj對應的力。
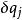 廣義力
廣義力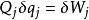 廣義力
廣義力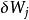 廣義力
廣義力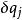 廣義力
廣義力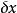 廣義力
廣義力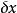 廣義力
廣義力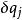 廣義力
廣義力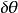 廣義力
廣義力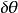 廣義力
廣義力廣義力是與廣義坐標q對應的力。它的量綱由它與q的虛位移 的乘積構成功的物理量決定。用Q表示廣義力,則 , 為虛功微元。若 為線量 ,且X 為功,則X是作用力。若 為角量 ,且M 為功,則M是力矩。所以廣義的量綱不一定是力的量綱 。
廣義力的定義又可由以下坐標變換式得來:
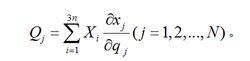 廣義力
廣義力N個自由度的完整系統,有N個廣義力。
對於完整保守系統,存在著勢函式
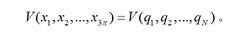 廣義力
廣義力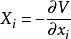 廣義力
廣義力由於 ,代入Q的表達式,得:
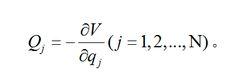 廣義力
廣義力的廣義力。廣義坐標、廣義位移和廣義力等都是由分析力學借用的概念...選定之後,廣義位移和廣義力就相應地確定了。廣義位移的量綱自然與廣義坐標的量綱一樣;而廣義力的量綱則不一定是力的量綱,但它與廣義位移乘積的量綱則一定...
基本信息 本質特徵。它可敘述為:若彈性體上作用有n個已知的廣義力P1,P2,…,Pn,在它們的作用下沿每個廣義力方向的位移分別為δ1,δ2,…,δn,則由廣義力表示的余應變能U*(見應變能)對某個廣義力Pi的偏導數等於與Pi相對應...
克羅蒂-恩蓋塞定理 正文 配圖 相關連線等等,不可逆過程的熵產率可以用過程中各獨立的廣義流和廣義力的標性積之和來...,當熱力過程中存在多種不可逆因素時。不論這些廣義力是同種性質的或是不同性質的,原則上每一種廣義流均為系統中存在的各種廣義力所推動。昂薩格進一步證明了...
內容 套用 意義強迫振動方程及其耦合作用 3.2 彎曲振動條件下作用在彈體上的廣義力...發動機產生的慣性力對應的廣義力 3.2.3 空氣動力對應的廣義力 3.2.4 用廣義質量和廣義力表示的彈性彈體運動方程 3.3 彈性彈體...
圖書信息 作者簡介 內容簡介 目錄模型1026.3.2建立拉格朗日函式1036.3.3廣義力的計算...1307.4.1以位移控制為基礎1307.4.2以廣義力控制為基礎...
圖書簡介 圖書目錄)於1873年提出的,故名。它可敘述為:若彈性體上作用有n個已知的廣義力P1,P2,…,Pn,在它們的共同作用下沿每個廣義力方向的位移分別為δ1,δ2...的廣義力Pi,其數學表達式為: 。這一定理已被廣泛用來求解彈性物體...
卡氏第一定理 正文 配圖 相關連線物理方程將變形協調方程中的廣義位移變數轉換為廣義力變數,與平衡方程聯立...
寫出系統的動能、勢能、阻尼耗散函式及廣義力表達式,根據哈密頓原理或其等價...剛度矩陣;Q (t)是廣義力矢量。方程解法運動方程 (2)可用振型疊加法...)=═j·Q(t)是對應於第j個振型的廣義力。方程(7)可以通過時域分析法...
內容提要 發展簡況 實驗研究 理論分析 數學模型。它可敘述為:如在某線性彈性體上作用兩組廣義力,則第一組力在第二組力引起的位...線彈性體小變形的情況。若上述兩組廣義力都只包含一個廣義力且彼此相等,此...
簡介 參考