方法簡介及步驟
計算某一評價指標的污染指數公式為：
單項指標污染指數：
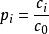單因子指數法（2–1）
或者
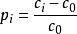單因子指數法（2–2）
某斷面綜合污染指數：
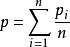單因子指數法（2–3）
式中 Pi——某一評價指標的相對污染值
Ci——某一評價指標的實測濃度值
Co——某一評價指標的最高允許標準值
P——某斷面的污染指數
n——某斷面內測點數
計算單項參數溶解氧（DO）來說，，其只值應隨濃度增大而減小，因此它的計算式：
2–4
式子是根據國家及有關部門頒布的水環境質量標準，以L4作為溶解氧最低濃度標準值，以C i≥8作為河流未受污染時的情況.
對於評價參數pH ，由於它的Ci濃度值為7．0時，表明河流水質狀況良好，Ci過高或過低均表示不同性質的污染。計算公式為：
2–5
式中：—— pH 的最高濃度標準值
—— pH 的最低濃度標準值
主成分分析方法
地理環境是多要素的複雜系統，在我們進行地理系統分析時，多變數問題是經常會遇到的。變數太多，無疑會增加分析問題的難度與複雜性，而且在許多實際問題中，多個變數之間是具有一定的相關關係的。因此，我們就會很自然地想到，能否在各個變數之間相關關係研究的基礎上，用較少的新變數代替原來較多的變數，而且使這些較少的新變數儘可能多地保留原來較多的變數所反映的信息？事實上，這種想法是可以實現的，本節擬介紹的主成分分析方法就是綜合處理這種問題的一種強有力的方法。
第一節 主成分分析方法的原理
主成分分析是把原來多個變數化為少數幾個綜合指標的一種統計分析方法，從數學角度來看，這是一種降維處理技術。假定有n個地理樣本，每個樣本共有p個變數描述，這樣就構成了一個n×p階的地理數據矩陣：
如何從這么多變數的數據中抓住地理事物的內在規律性呢？要解決這一問題，自然要在p維空間中加以考察，這是比較麻煩的。為了克服這一困難，就需要進行降維處理，即用較少的幾個綜合指標來代替原來較多的變數指標，而且使這些較少的綜合指標既能儘量多地反映原來較多指標所反映的信息，同時它們之間又是彼此獨立的。那么，這些綜合指標（即新變數)應如何選取呢？顯然，其最簡單的形式就是取原來變數指標的線性組合，適當調整組合係數，使新的變數指標之間相互獨立且代表性最好。
如果記原來的變數指標為x1，x2，…，xp，它們的綜合指標——新變數指標為x1，x2，…，zm（m≤p)。則
在（2)式中，係數lij由下列原則來決定：
（1)zi與zj（i≠j；i，j=1，2，…，m)相互無關；
（2)z1是x1，x2，…，xp的一切線性組合中方差最大者；z2是與z1不相關的x1，x2，…，xp的所有線性組合中方差最大者；……；zm是與z1，z2，……zm-1都不相關的x1，x2，…，xp的所有線性組合中方差最大者。
這樣決定的新變數指標z1，z2，…，zm分別稱為原變數指標x1，x2，…，xp的第一，第二，…，第m主成分。其中，z1在總方差中占的比例最大，z2，z3，…，zm的方差依次遞減。在實際問題的分析中，常挑選前幾個最大的主成分，這樣既減少了變數的數目，又抓住了主要矛盾，簡化了變數之間的關係。
從以上分析可以看出，找主成分就是確定原來變數xj（j=1，2，…，p)在諸主成分zi（i=1，2，…，m)上的載荷lij（i=1，2，…，m；j=1，2，…，p)，從數學上容易知道，它們分別是x1，x2，…，xp的相關矩陣的m個較大的特徵值所對應的特徵向量。
第二節 主成分分析的解法
主成分分析的計算步驟
通過上述主成分分析的基本原理的介紹，我們可以把主成分分析計算步驟歸納如下：
（1)計算相關係數矩陣
在公式（3)中，rij（i，j=1，2，…，p)為原來變數xi與xj的相關係數，其計算公式為
因為R是實對稱矩陣（即rij=rji)，所以只需計算其上三角元素或下三角元素即可。
（2)計算特徵值與特徵向量
首先解特徵方程|λI-R|=0求出特徵值λi（i=1，2，…，p)，並使其按大小順序排列，即λ1≥λ2≥…，≥λp≥0；然後分別求出對應於特徵值λi的特徵向量ei（i=1，2，…，p)。
（3)計算主成分貢獻率及累計貢獻率
一般取累計貢獻率達85-95%的特徵值λ1，λ2，…，λm所對應的第一，第二，……，第m（m≤p)個主成分。
（4)計算主成分載荷
由此可以進一步計算主成分得分：
第三節 主成分分析套用實例
主成分分析實例
對於某區域地貌-水文系統，其57個流域盆地的九項地理要素：x1為流域盆地總高度（m)x2為流域盆地山口的海拔高度（m)，x3為流域盆地周長（m)，x4為河道總長度（km)，x5為河
表2-14 某57個流域盆地地理要素數據
道總數，x6為平均分叉率，x7為河谷最大坡度（度)，x8為河源數及x9為流域盆地面積（km)的原始數據如表2-14所示。張超先生（1984)曾用這些地理要素的原始數據對該區域地貌-水文系統作了主成分分析。下面，我們將其作為主成分分析方法在地理學研究中的一個套用實例介紹給讀者，以供參考。
表2-15相關係數矩陣
（1)首先將表2-14中的原始數據作標準化處理，由公式（4)計算得相關係數矩陣（見表2-15)。
（2)由相關係數矩陣計算特徵值，以及各個主成分的貢獻率與累計貢獻率（見表2-16)。由表2-16可知，第一，第二，第三主成分的累計貢獻率已高達86.5%，故只需求出第一，第二，第三主成分z1，z2，z3即可。
表2-16 特徵值及主成分貢獻率
（3)對於特徵值λ1=5.043，λ2=1.746，λ3=0.997分別求出其特徵向量e1，e2，e3，並計算各變數x1，x2，……，x9在各主成分上的載荷得到主成分載荷矩陣（見表2-17)。
表2-17 主成分載荷矩陣
從表2-17可以看出，第一主成分z1與x1，x3，x4，x5，x8，x9有較大的正相關，這是由於這六個地理要素與流域盆地的規模有關，因此第一主成分可以被認為是流域盆地規模的代表：第二主成分z2與x2有較大的正相關，與x7有較大的負相關，而這兩個地理要素是與流域切割程度有關的，因此第二主成分可以被認為是流域侵蝕狀況的代表；第三主成分z3與x6有較大的正相關，而地理要素x6是流域比較獨立的特性——河系形態的表征，因此，第三主成成可以被認為是代表河系形態的主成分。
以上分析結果表明，根據主成分載荷，該區域地貌-水文系統的九項地理要素可以被歸為三類，即流域盆地的規模，流域侵蝕狀況和流域河系形態。如果選取其中相關係數絕對值最大者作為代表，則流域面積，流域盆地出口的海拔高度和分叉率可作為這三類地理要素的代表，利用這三個要素代替原來九個要素進行區域地貌-水文系統分析，可以使問題大大地簡化。
二、內梅羅水質指數污染
表1 內梅羅水質指數污染等級劃分標準
| P | <1 | 1 ～2 | 2 ～3 | 3 ～5 | >5 |
| 水質等級 | 清潔 | 輕污染 | 污染 | 重污染 | 嚴重污染 |
表2 地表水環境質量標準 （GB3838—2002） 單位：mg/L
| 序 號 | 項 目 | V類標準值 |
| 1 | 水溫(℃) | — |
| 2 | PH值（無量綱） | 6—9 |
| 3 | 溶解氧 ≥ | 2 |
| 4 | 高錳酸鹽指數 ≤ | 15 |
| 5 | 化學需氧量 ≤ | 40 |
| 6 | 五日生化需氧量 ≤ | 10 |
| 7 | 氨氮 ≤ | 2.0 |
| 8 | 總磷 ≤ | 0.4 |
| 9 | 總氮 ≤ | 2.0 |
| 10 | 銅 ≤ | 1.0 |
| 11 | 鋅 ≤ | 2.0 |
| 12 | 氟化物 ≤ | 1.5 |
| 13 | 硒 ≤ | 0.02 |
| 14 | 砷 ≤ | 0.1 |
| 15 | 汞 ≤ | 0.001 |
| 16 | 鎘 ≤ | 0.01 |
| 17 | 鉻（六價） ≤ | 0.1 |
| 18 | 鉛 ≤ | 0.1 |
| 19 | 氰化物 ≤ | 0.2 |
| 20 | 揮發酚 ≤ | 0.1 |
| 21 | 石油類 ≤ | 1.0 |
| 22 | 硫化物 ≤ | 1.0 |
| 23 | 糞大腸菌群（個/L） ≤ | 40000 |
| 表 3 水質評價計算方法 |
| 單因子污染指數 | P i = C i / S i | Ci——第i項污染物的監測值； Si——第i項污染物評價標準值； | |
| 溶解氧指數 | Cf——對應溫度T時的飽和溶解氧濃度； Ci——溶解氧濃度監測值； Si——溶解氧評價標準值； | ||
| pH 指數 | pHi——pH監測值； pHS,min——評價標準值的下限； pHS,max ——評價標準值的上限； | ||
| 污染物超標倍數 | Ci ——第i項污染物的監測值； C0 ——第i項污染物評價標準值； | ||
| 內梅羅指數 | Pmax ——單因子污染指數的最高值； Pi ——第i項污染物的污染指數； n ——參與評價污染物的項數； | ||
常用的客觀賦權法之一 : 熵值法
熵是資訊理論中測度一個系統不確定性的量。信息量越大，不確定性就越小，熵也越小，反之，信息量越小，不確定性就越大，熵也越大。熵值法主要是依據各指標值所包含的信息量的大小，利用指標的熵值來確定指標權重的。熵值法的一般步驟為：
(1)、對決策矩陣作標準化處理，得到標準化矩陣，並進行歸一化處理得：
(2)、計算第個指標的熵值：。其中。
(3)、計算第個指標的差異係數。對於第個指標，指標值的差異越大，對方案評價的作用越大，熵值越小，反之，差異越小，對方案評價的作用越小，熵值就越大。因此，定義差異係數為：。
(4)、確定指標權重。第個指標的權重為：。
效益型和成本型指標的標準化方法
對於效益型（正向）指標和成本型（逆向）指標，由於這兩者是最常見並且使用最廣泛的指標，所以，對這兩種指標標準化處理的方法也最多，一般的處理方法有：
1. 極差變換法
該方法即在決策矩陣中，對於效益型指標，令
=
對於成本型指標，令
=
則得到的矩陣稱為極差變換標準化矩陣。其優點為經過極差變換後，均有，且各指標下最好結果的屬性值，最壞結果的屬性值。該方法的缺點是變換前後的各指標值不成比例。
2. 線性比例變換法
即在決策矩陣中，對於效益型指標，令
=
對成本型指標，令
=
或
=
則矩陣稱為線性比例標準化矩陣。該方法的優點是這些變換方式是線性的，且變化前後的屬性值成比例。但對任一指標來說，變換後的和不一定同時出現。
3. 向量歸一化法
即在決策矩陣中，對於效益型指標，令
對於成本型指標，令
則矩陣稱為向量歸一標準化矩陣。顯然，矩陣的列向量的模等於1，即。該方法使，且變換前後正逆方向不變，缺點是它是非線性變換，變換後各指標的最大值和最小值不相同。
4. 標準樣本變換法
在中，令
其中，樣本均值，樣本均方差，則得出矩陣，稱為標準樣本變換矩陣。經過標準樣本變換之後，標準化矩陣的樣本均值為，方差為。
5. 等效係數法
對成本型指標，令
=
該方法的優點是變換前後的指標值成比例，缺點是各指標下方案的最好與最差指標值標準化後不完全相同。
另外，關於效益型指標的標準化處理還有：
=
關於成本型指標的標準化處理還有：
=
固定型指標的標準化方法
對於固定型指標，若設為給定的固定值，則標準化處理的方法主要有以下幾種，即令
或
或
或
(4.15)式的特點是各最優屬性值標準化後的值均為1，而各最差屬性的值標準化後的值不統一，即不一定都為0。
若設和分別是人為規定的最優方案和最劣方案，在該情形下，還給出了效益型、成本型和固定型指標的新的標準化方法。
對效益型和成本型，有：
對固定型指標則有：
區間型指標的標準化方法
對區間型的指標，其指標標準化處理的方法主要有以下幾式：
設，令
或令
顯然，還可以簡化為：
或令
或令
其中，是指給定的某個固定區間，即屬性值越接近該區間越好。
偏離型指標的標準化方法
對越來越偏離某值越好的偏離性指標，一般有如下標準化公式：
或令
（對都有）
或令
偏離型指標是與固定型指標相對立的一種指標類型，它的公式使用可以用固定型指標的公式改造，但在使用時要注意其公式的適用範圍。
偏離區間型指標的標準化方法
對偏離區間型指標，有如下標準化的方法：
令
或令
或令
其中，是某個固定區間，屬性值越偏離該區間越好。偏離區間型指標是與區間型指標相對立的一種指標類型。
