哈密頓圖

哈密頓通路（迴路）與哈密頓圖 （Hamilton圖） 通過圖G的每個結點一次，且僅一次的通路（迴路），就是哈密頓通路（迴路），存在哈密頓迴路的圖就是哈密頓圖。

基本信息

• 中文名稱：哈密頓圖
• 外文名：Hamiltonian graph
• 提出時間：1960年
• 套用學科：運籌學

• 國家：美國

判斷

哈密頓圖

判斷哈密頓圖是較為困難的。
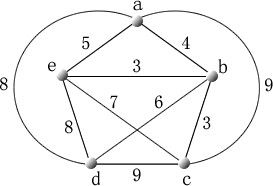哈密頓圖的充分條件和必要條件
⑴在無向簡單圖G=<V,E>中&frac12;V&frac12;&sup3;3,任意不同結點，則G是哈密頓圖（充分條件，定理4）。
⑵有向完全圖D=<V,E>；，若，則圖D是哈密頓圖（充分條件，定理5推論）。
⑶設無向圖G=<V,E>,"V1&Igrave;V，則P(G－V1）&pound;&frac12;V1&frac12；（必要條件，定理3）
若此條件不滿足，即$V1&Igrave;V，使得P(G－V!)>&frac12;V1&frac12；，則G一定不是哈密頓圖（非哈密頓圖的充分條件）。
哈密頓路徑也稱作哈密頓鏈，指在一個圖中沿邊訪問每個頂點恰好一次的路徑。尋找這樣的一個路徑是一個典型的NP-完全(NP-complete）問題。後來人們也證明了，找一條哈密頓路的近似比為常數的近似算法也是NP完全的。

算法級別

尋找哈密頓路的確定算法雖然很難有多項式時間的，但是這並不意味著只能進行時間複雜度為O(n!*n）暴力搜尋。利用狀態壓縮動態規劃，我們可以將時間複雜度降低到O（2^n*n^3），具體算法是建立方程f[i][S][j]，表示經過了i個節點，節點都是集合S的，到達節點j時的最短路徑。每次我們都按照點j所連的節點進行轉移。

美國圖論數學家奧勒在1960年給出了一個圖是哈密爾頓圖的充分條件：對於頂點個數大於2的圖，如果圖中任意兩點度的和大於或等於頂點總數，那這個圖一定是哈密頓圖。閉合的哈密頓路徑稱作哈密頓圈，含有圖中所有頂點的路徑稱作哈密頓路徑。