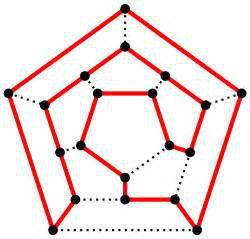
由來
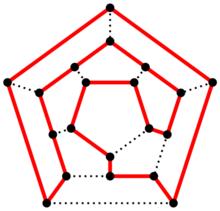 哈密頓迴路
哈密頓迴路天文學家哈密頓(William Rowan Hamilton) 提出,在一個有多個城市的地圖網路中,尋找一條從給定的起點到給定的終點沿 途恰好經過所有其他城市一次的路徑。
這個問題和著名的七橋問題的不同之處在於,過橋只需要確定起點,而不用確定終點。哈密頓問題尋找一條從給定的起點到給定的終點沿 途恰好經過所有其他城市一次的路徑。
算法
哈密頓路徑問題在上世紀七十年代初,終於被證明是“NP完備”的。據說具有這樣性質的問題,難於找到一個有效的算法。實際上對於某些頂點數不到100的網路,利用現有最好的算法和計算機也需要比較荒唐的時間(比如幾百年)才能確定其是否存在一條這樣的路徑。
從圖中的任意一點出發,路途中經過圖中每一個結點若且唯若一次,則成為哈密頓迴路。
要滿足兩個條件:
⒈封閉的環
⒉是一個連通圖,且圖中任意兩點可達
經過圖(有向圖或無向圖)中所有頂點一次且僅一次的通路稱為哈密頓通路。
經過圖中所有頂點一次且僅一次的迴路稱為哈密頓迴路。
具有哈密頓迴路的圖稱為哈密頓圖,具有哈密頓通路但不具有哈密頓迴路的圖稱為半哈密頓圖。
平凡圖是哈密頓圖。
⒊若以1到2、2到3、3到4、4到5、5到1,為計數規律,則各點均出現兩次;這種判斷方法在計算機編程運算中顯得尤為重要,其會精簡很多運算過程。
⒋新出爐,有待檢測的代碼如下:
註:這段代碼採用分支定界法作為編寫程式的依據,因此代碼依舊局限在算法上;而且代碼的使用對所要計算的數據是有要求的,如下:
⒈只要數據在開始計算出的n個最小值中,其重複次數超過2次的點的種類只能為一種,例如:代碼段中的數據五個最小值中其重複次數超過2次的點只有v5。
⒉數據矩陣格式要求:只允許為上三角矩陣,不支持全矩陣以及下三角矩陣的運算。
⒊代碼擴展方法請使用者獨立思考,不唯一。
⒋運算數據擴展方法,請使用者獨立思考,不唯一。
⒌此代碼為本人畢設的附加產品,不會對使用此代碼者,因理解不當或使用不當而造成的任何不良後果,付出任何責任。
⒍代碼僅供交流。