定義
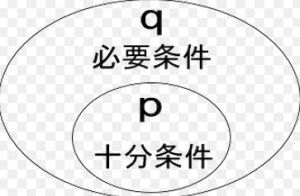 必要條件
必要條件例子
簡單地說,不滿足A,必然不滿足B;滿足A,不必然B,則A是B的必要條件。例如:1. A=“不斷呼吸”;B=“人能活著”。
2. A=“認識26個字母”;B=“能看懂英文”。
3. A=“聽過京劇”;B=“能體會到京劇的美”。
例子中A都是B的必要條件,確切地說,A是B的必要而不充分的條件:其一、A是B發生必需的;其二,A不必然導致B。在例子中,不呼吸人就不能活下去;認識了26個字母不一定就能看懂英文;聽過京劇未必能體會到京劇的美,這說明A不必然導致B。
生活中
生活中常用“只有……,才……”或“不……,不……”來表示必要條件。例如:1. 一個制度、一個政府,只有不斷地聽取批評意見,才能夠不斷改進工作,不斷進步。(溫家寶總理關於“問題奶粉”的談話)
2. 只有同心協力,才能把事情辦好。
3. 只有每年猶太歷七月初十日大祭司進入至聖所時,才能在約櫃前說出這個單詞的正確發音。
4. 人不犯我,我不犯人。
5. 不把這個殺人魔鬼處以極刑就不足以平民憤。
6. 沒有規矩,不成方圓。
生活中使用“只有……,才……”時人們往往並不考慮充分性。也就是說,不滿足A,必然不B成立時,我們就說,只有A,才B。這樣就表達了條件的必要性,至於條件A是否必然導致B我們沒有考慮。例如:
只有一個人觸犯了刑律,才可以依照刑法的規定處以刑罰。
從客觀上看,“觸犯了刑律”實際上是“可以依照刑法的規定處以刑罰”的充分必要條件。但是實際上說話人在說這句話時,他只想表達不滿足“觸犯了刑律”時就不能“依照刑法的規定處以刑罰”的意思。至於“觸犯了刑律要依照刑法的規定處以刑罰”的情況雖然大家都知道,但不是說話人要表達的意思。
所以生活中“只有……,才……”只是表達條件是必需的、必要的這個意思,而沒有考慮充分性,這和邏輯學的嚴格定義是不同的。
必要條件的其他說法:必要的條件、必需條件、必需的條件。“只有……,才……”表示的必要條件雖然“只有……,才……”句型表達條件的必要性,但很多時候它引出的條件不僅是必要的,也是充分的,實際上是充分必要條件。例如:
1. 只有用當年的葡萄榨取的葡萄汁為原料進行生產,葡萄酒才能標註上當年的年份。
2. 只有勞動者在試用期間被證明不符合錄用條件的,用人單位才可以解除勞動契約。
3. 由於對數字的迷信,西藏的修練者喜歡十二歲至十六歲的“智慧女”,根據宗喀巴,只有在找不到上述女子的時候,才可以採用二十歲的。
這三個例子中,條件既是必要的,也是充分的。所以,把句子裡的“只有”改成“只要”後仍然符合邏輯。但是兩種表達方式的語義是不同的。
“只有”強調必要性,忽略充分性,即強調“不是用當年的葡萄榨取的葡萄汁為原料進行生產,葡萄酒就不能標註上當年的年份”,而忽略“用當年的葡萄榨取的葡萄汁為原料進行生產,則葡萄酒能標註上當年的年份”。
假如把句子改成“只要用當年的葡萄榨取的葡萄汁為原料進行生產,葡萄酒就能標註上當年的年份”也符合邏輯。
“只要”強調充分性,忽略必要性,即強調“用當年的葡萄榨取的葡萄汁為原料進行生產,則葡萄酒能標註上當年的年份”,而忽略“不是用當年的葡萄榨取的葡萄汁為原料進行生產,葡萄酒就不能標註上當年的年份”。
這樣的例子在生活中並不罕見。例如:
這件事只有解釋一會兒他才明白。
這件事只要解釋一會兒他就明白了。
這兩句話有什麼不同呢?為什麼有時要強調必要性有時又強調充分性呢?
其實這取決於說話人的預設。預設是指暗含在語句中的一種預先設定的信息,在交際中通常表現為雙方都可理解、都可接受的那種背景知識。如:“他的筆丟了”預設“他有筆”。句子“這件事只有解釋一會兒他才明白”預設這件事比較複雜,一時半會說不清楚;句子“這件事只要解釋一會兒他就明白了”則預設這件事很簡單,一下就可以說明白。由於預設不同,說話人就使用不同的關聯詞。
最常見的情況是:“只有……,才……”預設“難、方法唯一”;“只要……,就……”預設“易”。
例子:只有你跟他面談才能把他說服。——難
只要你跟他面談就能把他說服。——易
邏輯學中
定義:如果沒有事物情況A,則必然沒有事物情況B;如果有事物情況A而未必有事物情況B,A就是B的必要而不充分的條件,簡稱必要條件。必要條件是邏輯學在研究假言命題及假言推理時引出的。
陳述某一事物情況是另一件事物情況的必要條件的假言命題叫做必要條件假言命題。必要條件假言命題的一般形式是:只有p,才q。符號為:p←q(讀作“p逆蘊涵q”) 。例如“只有有作案動機,才會是案犯”是一個必要條件假言命題。
根據必要條件假言命題的邏輯性質進行的推理叫必要條件假言推理。
數學中
有命題p、q,如果p推出q,則p是q的充分條件,q是p的必要條件;如果p推出q且q推出p,則p是q的充分必要條件,簡稱充要條件。例如:x=y推出x^2=y^2,則x=y是x^2=y^2的充分條件,x^2=y^2是x=y的必要條件(x為負數,y為正數時,不能推出x=y)。(x^2表示x的平方)
a、b一正一負推出ab<0,ab<0推出a、b一正一負,則a、b一正一負和ab<0互為充要條件。

