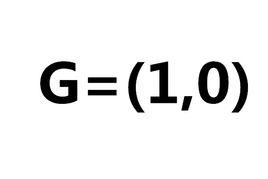定義
平凡圖的定義:
1.僅有一個結點的圖的稱平凡圖;
2.平凡圖是平凡樹;
3.邊的集合為空的圖叫做零圖,1階零圖叫做平凡圖,所謂n階圖是指有n個頂點的圖;
4.頂點的集合為空的圖叫做空圖。
圖的概念
現實世界中許多現象都可以用某種圖形表示,這些圖形由一些點和連線兩點的連線所組成,點表示事物,用點與點之間是否有連線表示事物之間是否有某種聯繫,這樣構成的圖形就是圖論中的圖。
一個圖是一個有序的二元組<V,E>,記作G,其中
 平凡圖
平凡圖(1)是有限非空集合,稱為頂點集,其元素稱為頂點或結點。
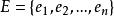 平凡圖
平凡圖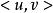 平凡圖
平凡圖(2)是有限集合,稱為邊集,E中每個元素都有V中的結點對與之對應,稱為邊。邊e既可以是有向的,也可以是無向的。有向邊與有序結點對對應,這時稱u為e的起點,v為e的終點。無向邊與無序結點對(u,v)對應,u,v稱為e的兩個端點。當e為有序對時.圖G是有向圖:當e為無序對時,圖G是無向圖。
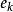 平凡圖
平凡圖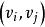 平凡圖
平凡圖(3)將圖的集合定義轉化成圖形表示之後,常用表示圖的邊.稱頂點或邊用字母標定的圖為標定圖,否則稱為非標定圖。
(4)將有向圖各有向邊均改成無向邊後的無向圖稱為原有向圖的基圖。
(5)若一條邊連線同一個點,稱其為圈或環。
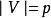 平凡圖
平凡圖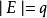 平凡圖
平凡圖(6)若,,則通常稱它為圖G(p,q)。p稱為圖G的階。圖G(1,0)稱為平凡圖。邊集E為空集的圖稱為零圖。頂點集V和邊集E都是有限集的圖稱為有限圖。
(7)若e=(u,v),則稱點u與點v相鄰接。並晚點u與邊e相關聯,點v與邊e相關聯。若u≠v,則稱e與u(或v)的關聯次數為1;若u=v,則稱e與u的關聯次數為2:若u不是e的端點,則稱e與u的關聯次數為0。同樣,若邊e和邊f有一個共同的端點,則也稱邊e和邊f相鄰接。沒有邊關聯於它的頂點稱為孤立點,不與其他任何邊相鄰接的邊稱為孤立邊。
平凡樹
平凡圖稱為平凡樹。樹是圖論中重要內容之一,在計算機科學技術中有著廣泛的套用。樹的概念由數學家約當(Jordan)給出了統一的定義。一個無圈的連通圖稱為樹,樹中點的個數稱為該樹圖的階,且稱次為1的點為懸掛點.與之相鄰的邊稱為懸掛邊,僅一個點的圖可視為平凡樹。
樹的定義
連通且無迴路的無向圖稱為無向樹,或簡稱樹,常用T表示樹。平凡圖稱為平凡樹。無向樹中度數為1的頂點稱為樹葉,度數大於等於2的頂點稱為分支點:若無向樹T至少有兩個連通分支,則稱T為森林。
也就是說,(無向)樹是連通無迴路的簡單圖,後面提到樹時,如果沒有特別說明都是指無向樹,樹的每一條邊都是橋。
相關概念
1. 若圖G是平凡圖或G中任意兩點都是連通的,則稱圖G為連通圖,否則稱G為非連通圖或分離圖。
2. 如果圖G的頂點集的一個真子集T滿足G一T不連通或是平凡圖,則稱T為G的一個點割(vertex cut)。如果圖G的邊集的一個真子集S滿足G-S不連通或是平凡圖,則稱S為G的一個邊割(edge cut)。
3. 連通圖:如果無向圖G中每一對不同的結點x和y間都有一條路(即W((G)=1),則稱G是連通網(connected digraph or graph).否則稱為非連通圖(disconnected graph)。
4. 設G=<V,E>為無向圖,頂點u,v∈V,若u,v之間存在通路,則稱頂點u和v是連通的,記作u~v,並規定u與自身是連通的。若無向圖G=<V,E>是平凡圖或G中任何兩個頂點都是連通的.則稱G是連通圖,否則,稱G為非連通圖或分離圖。