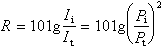方程推導
又稱典型系統或正則系統或哈密頓典型系統(方程)，常簡記為H.S.。指如下形式的一階微分方程系統
推導過程是由英國科學家W.R.哈密頓於1835年引進，廣泛套用於力學、物理學,形成了一整套的理論。上式中的 p稱為廣義衝量（或動量）， q稱為廣義坐標，( p, q)稱為共軛變數，也稱為典型變數， q空間稱為構形空間，( p, q)空間稱為相空間， H 則稱為哈密頓函式。
如 H 中不含 t，則(*)稱保守系統；此時，
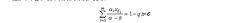推導過程h= C
推導過程為系統的一個初積分，例如， T為動能， V為勢能,則 h= T+ V= C表能量守恆定律。如 H 中含 t，取 t= qn+1，並取,即可得到不含 t的 啛 的H.S.：
推導過程所以， H 中不含 t的哈密頓系統具有一定的廣泛性。
（J.-）H.龐加萊曾在他的名著《天體力學新方法》(1892～1899)中暗示許多力學中的微分方程系統都可化成H.S.,但他只舉出一些例子,沒有證明。後來P.A.M.狄喇克證明下述結果(1935)，對龐加萊的暗示作了很好的補充。設有,令即得H.S.:，。因此，研究H.S.理論就是研究一般的一階正規型微分方程系統，只是引進了餘切空間( y1, y2,…, yn)而已。
當 H= H0( p)，即只含 p時，稱為可積系統。因為,而，從而，當 q為角變數時，積分曲線在 p= p0環面上。
典型變換
推導過程
推導過程卡姆 (KAM)理論
關於哈密頓系統方程組的解的穩定性理論。是由A.H.柯爾莫哥洛夫，Β.И.阿爾諾德和J.K.莫澤三人共同建立的(1954、1963)，因而得名。他們嚴格證明了擬周期解的存在性，即幾乎可積系統，有填滿不變環的擬周期解存在。這是哈密頓系統，特別是它的定性理論的近代發展中的最重要的成就。
1889年由龐加萊所開創的哈密頓系統的定性理論中最深刻的結果是限制性三體問題中近圓形軌道的穩定性，這個結果的證明即來自KAM理論，從而使P.-S.拉普拉斯提出的,已歷時200年的太陽系穩定性問題得到重要的突破。無論從微分方程方面，或從天體力學方面來看，這都是重大的貢獻，得到廣泛重視。
KAM理論很複雜，它的思想略述如下。
推導過程把變換倒過來，( P, Q)→…→( p, q)，在一定條件下，有些環面只是被了，但並沒有破裂。積分曲線中有的還在被扭曲了的環面上。特別，當環面是三維空間的環面，則積分曲線被圍困在兩相鄰環面之間，無法逸出，顯示出運動的拉格朗日穩定性。
