哈密頓正則方程

哈密頓正則方程

正文

經典力學中一組描寫系統運動的一階微分方程組。是W.R.哈密頓於1834年提出的，又稱哈密頓方程或正則方程。哈密頓正則方程為

(1)

式中H稱為哈密頓函式,是廣義動量pi和廣義坐標qi及時間t的函式。H由式

(2)

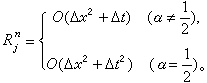確定。括弧外邊的角標表示式中的妜i應該用N個方程pi= 解出N 個 妜i為 (E1,E2,…,EN；q1,q2,…,qN；t)的N 個函式，然後代入式(2)就得到哈密頓函式H。
對於直角坐標變換到廣義坐標的變換式雖然顯含時間t，但是動能的表示式不明顯地包含t，此時

H＝T2-T0+V,

式中T2和T0可說明如下：用(E1,E2,…,EN；q1,q2,…，qN；t)表示的動能式T＝T2+T1+T0,式中T2、T1和T0分別表示廣義動量的二次齊次式、一次齊次式和不含廣義動量的項。
如果直角坐標變換到廣義坐標的變換式不顯含t,勢函式V也不顯含t，則

T＝T2，H＝T+V。

即對於保守系統，哈密頓函式是系統總機械能用廣義動量表示的公式。
正則方程式(1)是2N個一階微分方程組,而拉格朗日方程是N個二階微分方程組,都只適用於完整系統（見約束）的動力學方程組。
由於式(1)的左邊不再有變數q和p的導數,所以方程(1)成為如下形式的方程組

保守系統的正則方程在天體力學和經典統計力學中有重要的套用。在天體力學中從可解的二體問題出發，逐漸添加其他星球的引力，可以把所用的哈密頓函式H，從簡單改變成較複雜的 H┡。這是天體力學中的攝動法，用來解決考慮太陽和各種行星、衛星的引力作用下的行星運動，由此可制定行星和月球的星曆表，在統計力學中的劉維定理就是套用正則方程推導出來的。

配圖

相關連線