簡介
佩蒂斯積分亦稱弱積分,是一種常用的向量值函式的積分,此積分是佩蒂斯(Pettis,P. B.J. )於1938年建立的。
 佩蒂斯積分
佩蒂斯積分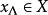 佩蒂斯積分
佩蒂斯積分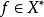 佩蒂斯積分
佩蒂斯積分設(Ω,,μ) 為σ有限測度空間,x(t) 是定義在Ω上而取值於巴拿赫空間X的弱可測向量值函式,如果對任意 A ,都存在 ,使得對於一切 ,積分
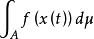 佩蒂斯積分
佩蒂斯積分存在,且
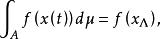 佩蒂斯積分
佩蒂斯積分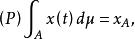 佩蒂斯積分
佩蒂斯積分則說x(t) 在Ω 上佩蒂斯可積,此時記為 並稱 X 為x(t) 在 A 上的佩蒂斯積分。
性質
 佩蒂斯積分
佩蒂斯積分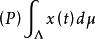 佩蒂斯積分
佩蒂斯積分當x(t)在Ω上佩蒂斯可積時,在每個A上,佩蒂斯積分是惟一確定的。
除去富比尼定理外,勒貝格積分的其他性質對於佩蒂斯積分也成立。例如,佩蒂斯積分作為向量值集函式具有絕對連續性和可列可加性,對於被積函式具有線性性質。
如果向量值函式x(t)是博赫納可積的,則它也是佩蒂斯可積的。並且,該兩積分值是相同的,但反之不然。
又如,佩蒂斯可積的函式必是蓋爾范德可積的,當X是自反的巴拿赫空間時,這兩種積分彼此相同。
