定義
定義 ：
勢函式滿 足 以 下 條 件 的連 續 函式稱 為 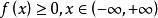勢 函式 ：
勢函式(1 ).
勢函式 勢函式
勢函式
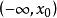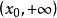勢函式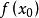 勢函式
勢函式(2 ) 存 在 , 使得 在上單調遞增，在上單調遞減，並稱為此勢函式的中心點，為此勢函式的高度 。
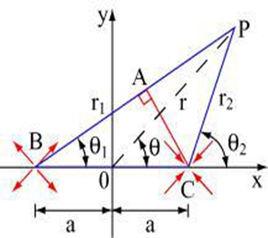
典型的勢函式構造方法：P(θ)=f{d(θ,θ),[dR(θ),O],dT}(1)，式中 θ，θ——機器人當前位姿與目標位姿矢量；d(θ,θ)——θ與θ間的某種廣義距離函式；dR(θ)，O——當前位姿下機器人與障礙物間的最小距離；dT——給定的門限值；P(θ)分別為變數d(θ,θ)和dR(θ)，O的單調遞增函式和單調遞減函式。
對勢模型
在 20 世紀 80 年代以前 ,分子動力學模擬一般都採用對勢模型。對勢可以比較好地描述除金屬和半導體以外的幾乎所有無機化合物。有些對勢是經過一定的理論分析而得到的，但其中一些參數則需要根據巨觀實驗參數用經驗方法來確定，這些巨觀實驗參數主要有彈性常數、平衡點陣常數以及內聚能、空位形成能和層錯能等，這些稱為半經驗勢。後來，為了擬合的方便，人們在選擇勢函式的形式時，並不一定要求有確切的理論依據，而是出於經驗的估計和擬合方便的需要，相對自由地選擇勢函式形式 ，這樣確定的勢函式被稱為經驗勢 。.
幾種典型的的半經驗勢
1、Lennard-Jones勢
Lennard-Jones 勢函式的解析表達式可寫為 ：
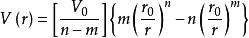勢函式。
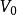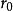勢函式
勢函式其中 ， 反映了相互作用的強度； 反映了原子的大小。根據量子力學二次微擾論的偶極子-偶極子相互作用可導出 n =12 ，這一項描述了范德瓦耳斯力 .後一項是排斥力 ，其來源之一是原子核之間的庫侖斥力，來源之二是電子之間由於泡利不相容原理產生的交疊能。
2、Morse 勢
1929 年，Morse 注意到雙原子分子的振動譜的量子力學問題可用指數形式的勢函式解析地解決 ，並發現計算結果與實驗一致 。於是他提出如下形式的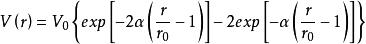勢函式 ：
勢函式。
Mo rse 勢和 Lennard-Jones 勢的曲線形式非常相似。M orse 勢常常用來構造各種多體勢的對勢部分。
3、Born —Mayer 勢
Born 和 M ayer 估計鹼金屬離子之間的排斥項可用指數形式表示，於是提出如下形式的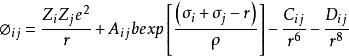勢函式：
勢函式。
