定理敘述
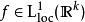勒貝格微分定理
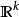勒貝格微分定理 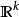勒貝格微分定理設 為局部可積函式，m為 的勒貝格測度。那么 中幾乎處處的x都符合 。
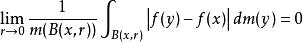勒貝格微分定理證明
因為這定理是關於函式的局部性質，不失一般性，可假設函式 f定義在有界集合中，故 f為可積函式。
定義
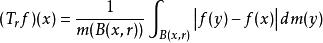勒貝格微分定理
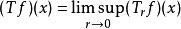勒貝格微分定理那么這定理就是對幾乎處處的x有Tf= 0。只需證對任何y> 0，集合{Tf>y}的測度為零。
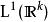勒貝格微分定理
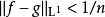勒貝格微分定理對連續函式，這定理顯然成立。連續函式在 中稠密，故此對任意正整數n，有連續函式g使得 。
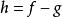勒貝格微分定理令 。由於g連續，有Tg= 0。
用三角不等式有
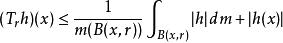勒貝格微分定理
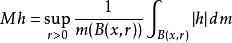勒貝格微分定理設 。（ Mh為 h的哈代－李特爾伍德極大函式。）從上式得
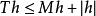勒貝格微分定理
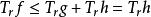勒貝格微分定理因為 ，所以有
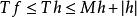勒貝格微分定理
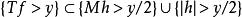勒貝格微分定理若 Tf> y，則有 Mh> y/2或者| h| > y/2。因此
由哈代－李特爾伍德極大不等式得
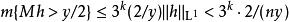勒貝格微分定理
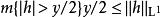勒貝格微分定理
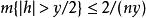勒貝格微分定理由積分的基本性質有 ，故得 。因此
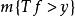勒貝格微分定理
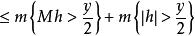勒貝格微分定理
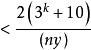勒貝格微分定理因為上式對所有正整數 n成立，從而知 m{ Tf> y}=0。定理得證。
