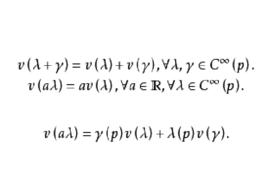知識儲備
在定義切向量之前,首先給出光滑函式的定義。敘述中都將按國際非線性學術界表達慣例,向量將一律用白斜體字母表示 。
 切向量
切向量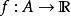 切向量
切向量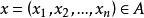 切向量
切向量 切向量
切向量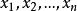 切向量
切向量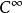 切向量
切向量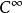 切向量
切向量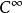 切向量
切向量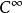 切向量
切向量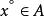 切向量
切向量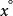 切向量
切向量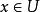 切向量
切向量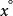 切向量
切向量 切向量
切向量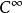 切向量
切向量定義1 設A是 的一個開子集(即A內每點都可找到一個完全屬於A的鄰域), 是一個函式。f點z 的值記為 。如果f對 的任意階偏導數存在且連續,則稱函式f是 類函式(function of class ),簡稱f是一個 函式或稱f是一個光滑函式(smooth function)。如果函式f是 的,且對任意指定點 ,存在 的一個鄰域U,使對所有 ,f在 的Taylor級數展開式都收斂到 ,則稱f是一個 函式或稱f 是一個解析函式( analytic function)。
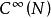 切向量
切向量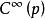 切向量
切向量定義2 一流形N上有定義的所有光滑函式的集合,記為 。在流形N上一點p的鄰域有定義的所有光滑函式的集合,記為 。
定義
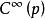 切向量
切向量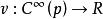 切向量
切向量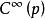 切向量
切向量設N是一個n維光滑子流形, 是在N上p點有定義的光滑函式集合, 是定義在 上的泛函(運算元),如果v有下列性質(也稱求導性質) :
(1)線性性
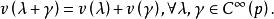 切向量
切向量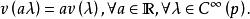 切向量
切向量(2)符合Leibnitz規則
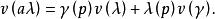 切向量
切向量則稱v是定義在流形N上某點p的一個 切向量(tangent vector)。
相關概念介紹
下面對以上定義作一些概念性說明 。
(1)流形(manifold)是拓撲學和微分幾何中的重要概念。不過,為不涉及過多的數學基礎,此處不準備作嚴格的定義。從概念上說,一個n維流形可理解為由多個同為n維的曲面(或超曲面)經拼接所得到的曲面(或超曲面)。
(2)流形的一個特徵是,它的一個局域可以與一個n維歐氏空間之間建立起點與點間的一對一映射關係,它的每個局域可以分別與各自的一個n維歐氏空間之間建立起點與點間的一對一映射關係,並可在此基礎上建立起通用於各局域的流形局部坐標系,從而變成可度量的( metrizable)。
(3)具有微分結構的流形被稱為微分流形(differential manifold)。這裡所說的微分結構,是指參與拼接的曲面(或超曲面)彼此拼接得是如此之好,以至於流形作為一整體與n維歐氏空間之間的映射能達到任意次可微的程度,即達到光滑的程度。因此微分流形也稱為光滑流形(smooth manifold)或簡稱流形。微分流形可理解為是由多個同為n維的光滑曲面(或超曲面)經拼接所得到的光滑曲面(或超曲面),也就是有任意階導數的n維曲面(或超曲面)。
 切向量
切向量(4)定義在流形N上的光滑函式 就是定義在流形N的局部坐標繫上的函式。對於一個光滑流形而言,其各階導數都存在。
 切向量
切向量 切向量
切向量(5)光滑函式 在某方向上的變化率,一般稱為方嚮導數(directional derivative)。方嚮導數取值是一實數。運算元v表示求方嚮導數的操作,故其映射關係可表示為 。
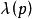 切向量
切向量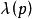 切向量
切向量(6)求導的方向在函式 的定義域上表示,即指的是流形局部坐標平面(或超平面)上定的方向,而不是指在 曲面的切平面(或超切平面)上定的方向。
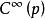 切向量
切向量 切向量
切向量切向量和方嚮導數有密切關係,但這是兩個不同的概念。切向量被定義為一個抽象的泛函(運算元),指的是 至歐氏空間 的一個映射,而方嚮導數則指的是該映射的像值 。
例題解析
 切向量
切向量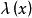 切向量
切向量 切向量
切向量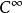 切向量
切向量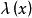 切向量
切向量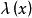 切向量
切向量(流形 上的切向量,切向量和方嚮導數的差異)設 是定義在 上的 (光滑)函式 在點x的方嚮導數(即 在定義域一定方向上的坡度或變化率)定義為
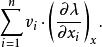 切向量
切向量 切向量
切向量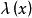 切向量
切向量式中, 是表示方向的係數。方向可以是給定的方向,也可以是某個體現函式 自身性質的方向。
 切向量
切向量比如, 在點x的梯度(gradient)被定義為向量
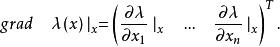 切向量
切向量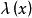 切向量
切向量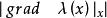 切向量
切向量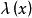 切向量
切向量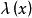 切向量
切向量在點x的方嚮導數在此方向有最大坡度值 ,梯度方向是 上升最陡的方向,所體現的就是函式 自身的性質。
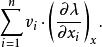 切向量
切向量如果把式 改寫成
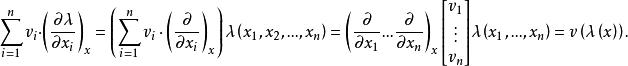 切向量
切向量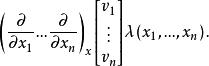 切向量
切向量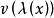 切向量
切向量註:其中中的三部分分別為切向量的基底、方向向量、光滑函式,這三部分組成一個切向量;為方嚮導數。
可見方嚮導數可拆成三部分。方嚮導數的前面兩部分,即切向量的基底和方向向量合稱為切向量。此切向量完全符合切向量定義。
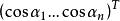 切向量
切向量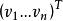 切向量
切向量方向的表示方法一般有兩種。一種是用方向餘弦向量表示,另一種是用方向數向量表示。切向量的方向一般都用後一種表示。方向數向量歸一化後等於方向餘弦向量。也可以說方向數向量等於方向餘弦向量外乘一個常數。該常數表示向量的長度或大小。所以通常所說的方向向量不僅指方向,還可能包括其長度。切向量的方向和大小都是點的函式。在不同點上,不僅方向可能不同,而且外乘的常數(向量的長度)也可能會隨之不同。儘管方向數向量有外乘常數,不僅表示方向,但為方便,以後仍將把它們和方向餘弦向量一樣看待,一律籠統地稱為方向向量。