簡介
在幾何中,以一般化的觀點來說,標量是零維的幾何量,向量是一維的有向幾何量,依此類推,我們可以有二維的有向幾何量。幾何代數中的外代數(exterior algebra)採用了這個一般化的觀點定義了 二重向量(bivector)。一個二重向量亦即二維的有向幾何量,它是一個有向面積。
二重向量是使用外積(exterior product)來產生的:令 a與 b為向量,它們的外積 a∧ b即為一個二重向量,代表由 a與 b圍成的平行四邊形面積,其方向為 a到 b的時針方向。所以,外積是反對稱的, a∧ b的方向恰與 b∧ a相反。另外, a∧ a是一個“零二重向量”。
有時候,三維的二重向量被拿來當作一種偽向量。
歷史
德國數學家赫爾曼·格拉斯曼於1844年的《線性外代數》論文中,將二重向量以二向量外積的方式介紹出來。同時期,愛爾蘭數學家威廉·哈密頓於1843年發表了四元數。1888年,英國數學家威廉·金頓·克利福德結合二者並發表了克利福德代數,二重向量才被完整的了解。
赫爾曼·格拉斯曼
赫爾曼·京特·格拉斯曼( Hermann Günther Graßmann,1809年4月15日-1877年9月26日),出生於什切青,是一個德國博學者,在他生活的時代以語言學家身份聞名,以數學家身份而著稱。他也是一位物理學家,新人道主義者,博學的學者,和出版家。
克利福德代數
克利福德代數( Clifford algebra),又稱 幾何代數( Geometric algebra),是綜合了內積和外積兩種運算,在幾何和物理中在很多套用的一門數學學科。克利福德代數是複數、四元數和外代數的推廣。
外代數
外代數(英語:Exterior algebra)也稱為 格拉斯曼代數(Grassmann algebra),以紀念赫爾曼·格拉斯曼。
數學上,給定向量空間 V的外代數,是特定有單位的結合代數,其包含了 V為其中一個子空間。它記為 Λ( V) 或 Λ( V)而它的乘法,稱為 楔積或 外積,記為∧。楔積是結合的和雙線性的;其基本性質是它在 V上交錯的,也就是:
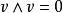 二重向量
二重向量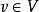 二重向量
二重向量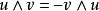 二重向量
二重向量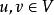 二重向量
二重向量 二重向量
二重向量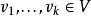 二重向量
二重向量,對於所有向量 ,這表示 ,對於所有向量 ,以及 ,當 線性相關時。
注意這三個性質只對 V中向量成立,不是對代數Λ( V)中所有向量成立。外代數事實上是“最一般的”滿足這些屬性的代數。這意味著所有在外代數中成立的方程只從上述屬性就可以得出。
形式為v∧v∧…∧v的元素,其中v,…,v在V中,稱為 k-向量。所有k-向量生成的Λ(V)的子空間稱為V的 k-階外冪,記為Λ(V)。外代數可以寫作每個k階冪的直和:
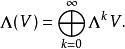 二重向量
二重向量該外積有一個重要性質,就是k-向量和l-向量的積是一個k+l-向量。這樣外代數成為一個分次代數,其中分級由k給出。這些k-向量有幾何上的解釋:2-向量u∧v代表以u和v為邊的帶方向的平行四邊形,而3-向量u∧v∧w代表帶方向的平行六面體,其邊為u,v, 和w。
外冪的主要套用在於微分幾何,其中他們用來定義微分形式。因而,微分形式有一個自然的楔積。所有這些概念由格拉斯曼提出。
偽矢量
 二重向量
二重向量偽矢量(英語:Pseudovector),指的是在瑕旋轉下,除了隨之反射外,還會再上下翻轉的矢量(因為右手定則的關係)。 矢量(極矢量)和偽矢量(軸矢量)都是廣義上的矢量,在一般旋轉下的特性相同。但更嚴格地說,矢量還要求在瑕旋轉下,除了空間反衍外,不會再改變方向。在三維空間中,偽矢量 p可以表示為二個極矢量 a和 b的外積: 以此方式計算的 p是偽矢量,其中一個例子是有向平面的法矢量。有向平面可以用二個不平行的矢量 a和 b來定義。矢量 a× b垂直此平面(和平面垂直的矢量有二個,其方向恰好相反,可以用右手定則決定是哪一個),為一偽矢量。許多物理量是偽矢量,例如磁感應強度、角速度等。在數學上,偽矢量是三維的二重矢量,可以由此推得偽矢量的轉換規則。 n維幾何代數的偽矢量是 n− 1維代數的元素,可以表示為Λ R。可以由偽矢量引申出偽標量及偽張量,在瑕旋轉下會比標量及張量多出一個負號。
