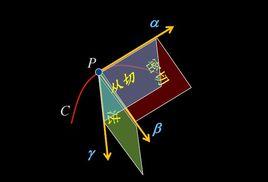
一、從切平面定義
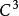從切平面給出 類空間曲線（C）和（C)上一點P，設曲線的（C）的自然參數表示為 ：
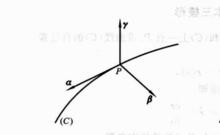空間曲線的基本向量
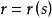從切平面其中s是自然參數，定義：
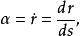從切平面
從切平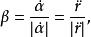面
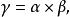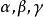從切平面
從切平面分別為曲線上P點的單位切向量，主法向量和副法向量。P點上的三個向量構成右手系。
從切平面
從切平面則 和 所確定的平面是曲線（C）上P點的從切平面。
二、從切平面方程
1、自然參數方程
如定義，從切平面方程為：
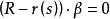從切平面或
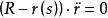從切平面2、一般參數方程
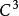從切平面給定 類空間曲線（C）
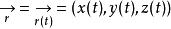從切平面
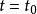從切平面則曲線C在一點 處的從切平面為：
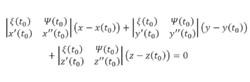從切平面其中
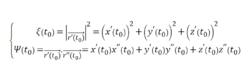從切平面三、計算實例
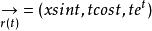從切平面1、求曲線 在原點的從切平面：
解:
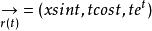從切平面
從切平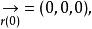面,
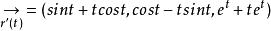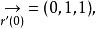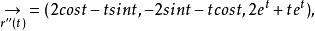從切平面
從切平面,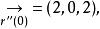
從切平面
從切平面ξ(0)=2,Ψ(0)=2
所以，從切平面方程為
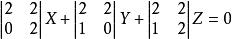從切平面即
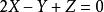從切平面四、性質及意義
1、從切平面，法平面，密切平面所構成的圖形稱為曲線的基本三棱形。
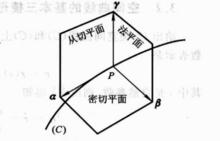空間曲線的基本三棱形
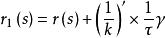從切平面2、曲線r(s)的密切球面與從切平面的交線圓的圓心軌跡方程
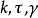從切平面其中分別為曲線的曲率，擾率和副法向量。
3、兩條曲線的對應點的從切平面重合，則這兩條曲線為達布曲線。
