線性空間
線性空間亦稱向量空間。它是線性代數的中心內容和基本概念之一。設V是一個非空集合,P是一個域。若:
1.在V中定義了一種運算,稱為加法,即對V中任意兩個元素α與β都按某一法則對應於V內惟一確定的一個元素α+β,稱為α與β的和。
2.在P與V的元素間定義了一種運算,稱為純量乘法(亦稱數量乘法),即對V中任意元素α和P中任意元素k,都按某一法則對應V內惟一確定的一個元素kα,稱為k與α的積。
3.加法與純量乘法滿足以下條件:
1) α+β=β+α,對任意α,β∈V.
2) α+(β+γ)=(α+β)+γ,對任意α,β,γ∈V.
3) 存在一個元素0∈V,對一切α∈V有α+0=α,元素0稱為V的零元.
4) 對任一α∈V,都存在β∈V使α+β=0,β稱為α的負元素,記為-α.
5) 對P中單位元1,有1α=α(α∈V).
6) 對任意k,l∈P,α∈V有(kl)α=k(lα).
7) 對任意k,l∈P,α∈V有(k+l)α=kα+lα.
8) 對任意k∈P,α,β∈V有k(α+β)=kα+kβ,
則稱V為域P上的一個線性空間,或向量空間。V中元素稱為向量,V的零元稱為零向量,P稱為線性空間的基域.當P是實數域時,V稱為實線性空間.當P是複數域時,V稱為複線性空間。例如,若V為三維幾何空間中全體向量(有向線段)構成的集合,P為實數域R,則V關於向量加法(即平行四邊形法則)和數與向量的乘法構成實數域R上的線性空間。又如,若V為數域P上全體m×n矩陣組成的集合Mmn(P),V的加法與純量乘法分別為矩陣的加法和數與矩陣的乘法,則Mmn(P)是數域P上的線性空間.V中向量就是m×n矩陣。再如,域P上所有n元向量(a1,a2,…,an)構成的集合P對於加法:(a1,a2,…,an)+(b1,b2,…,bn)=(a1+b1,a2+b2,…,an+bn)與純量乘法:λ(a1,a2,…,an)=(λa1,λa2,…,λan)構成域P上的線性空間,稱為域P上n元向量空間。
線性空間是在考察了大量的數學對象(如幾何學與物理學中的向量,代數學中的n元向量、矩陣、多項式,分析學中的函式等)的本質屬性後抽象出來的數學概念,近代數學中不少的研究對象,如賦范線性空間、模等都與線性空間有著密切的關係。它的理論與方法已經滲透到自然科學、工程技術的許多領域。哈密頓(Hamilton,W.R.)首先引進向量一詞,並開創了向量理論和向量計算。格拉斯曼(Grassmann,H.G.)最早提出多維歐幾里得空間的系統理論。1844—1847年,他與柯西(Cauchy,A.-L.)分別提出了脫離一切空間直觀的、成為一個純粹數學概念的、抽象的n維空間。特普利茨(Toeplitz,O.)將線性代數的主要定理推廣到任意域上的一般的線性空間中。
切向量
向量(切向量)存在多種定義。直觀的講,如果所研究的流形是一個三維空間中的曲面,則在每一點的切向量,就是和該曲面相切的向量,切空間就是和該曲面相切的平面。通常情形下,因為所有流形可以嵌入歐幾里得空間,切空間也可以理解為在該點和流形相切的歐幾里得空間的仿射子空間。切空間更好的定義不依賴於這種嵌入,例如,切向量可以定義為通過該點的曲線的等價類,或者是對光滑函式在該點的在某個方向上的求導。但所有這些定義都是等價的。
設M是可微的流形,p是M上一點, p處所有切向量全體張成的線性空間稱為M在p處的切空間, 記為T_p(M). 如果p是光滑點,則T_p(M)的維數就是流形M的維數。
切空間詳細定義
切空間是微分流形在一點處所聯繫的向量空間,歐氏空間中光滑曲線的切線、光滑曲面的切平面的推廣。若M是n維微分流形,p∈M,記C∞(p)為在p的某個鄰域內有定義的C∞可微函式的集合,則適合下列條件的函式X:C∞(p)→R稱為M在p處的切向量:
1.對於f,g∈C∞(p),若存在M中p的某鄰域U,使得f|U=g|U,則X(f)=X(g).
2.對於f,g∈C∞(p),α,β∈R,有:
 切空間
切空間這時C∞(p)中函式的運算依定義:
(αf+βg)(q)=αf(q)+βg(q)∈R,當f(q),g(q)有定義時。
3.對於f,g∈C(p),有:X(f×g)=f(p)X(g)+g(p)X(f),
其中f×g是通常函式的乘法,即:(f×g)(q)=f(q)g(q)。
微分流形M在p∈M處的全體切向量的集合記為TM,對於X,Y∈TM,α∈R與f∈C∞(p),設:
 切空間
切空間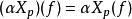 切空間
切空間因而TM是實數域R上的n維向量空間,稱為微分流形M在p處的切空間。
切空間TM中切向量的表示:設(U,φ)是M含點p的卡,在U上局部坐標為:
 切空間
切空間對於i=1,2,…,n,若:
 切空間
切空間 切空間
切空間其中(u,u,…,u)是R^n中坐標,則:
 切空間
切空間並且:
 切空間
切空間是TM的一組基。此時對於X∈TM,有:
 切空間
切空間
