設是一個格,若對於任意的有
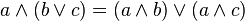
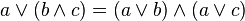
則稱L為分配格。
上述兩個等式互為對偶式,根據格的對偶原理,在證明一個格是分配格時只需證明其中任意一個等式即可。
設是一個格,L為分配格當且僅當對於任意的,若且,則b=c。
分配格設〈A,,〉是由格〈A,〉所誘導的代數系統。如果對任意的a,b,cA,滿足a(bc)=(ab)(ac)和a(bc)=(ab)(ac),則稱〈A,〉是分配格。
設是一個格,若對於任意的有
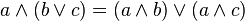
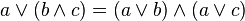
則稱L為分配格。
上述兩個等式互為對偶式,根據格的對偶原理,在證明一個格是分配格時只需證明其中任意一個等式即可。
設是一個格,L為分配格當且僅當對於任意的,若且,則b=c。
內容介紹《分配格序代數(英文版)》內容簡介:With the development of information science and theoretical computer science...
、濾子、同餘,Galois聯絡等;第3章論述了分配格的基本內容,著重討論了分配格的表示定理,分配格中的理想和同餘,Boole代數以及...結構;第5章闡述了完全分配格的性質和基本結構定理,以及完全分配格範疇的乘積...
內容介紹時發現的,也是最早研究的格,有補的分配格稱為布爾格,若布爾格僅含一個元素...分配格,那么A被稱為有補分配格 。定理 設 A,≤,∨,∧ 是一個有補分配格,A上每個元素都有唯一補元。證明 有補格一定存在全上界1,和全下界0...
基本介紹 定義 相關定理相關定理定理1設 L,≼ 是有界格且是分配格,a∈L,若a在L中有補元... 因此,有補分配格中毎一個元素有且只有一個補元,於是,若 L,≼ 是有補分配格, L,∨,∧ 是它透導的代數系統,則可在L中定義一種“補”的一元送...
基本介紹 相關定理的理想概念的數學結構可獲得其他定理,例如環和(環論的)素理想,和分配格和...陳述等價於 BPI 的事實可以輕易的從下列定理中看出: 對於任何分配格...理想的文章內。因為任何布爾代數都是分配格,這證實了想要的蘊涵。 所有...
初涉 素理想定理 布爾素理想定理 進一步的素理想定理 超濾子引理布爾格)是有補分配格(可參考格的定義)可以按各種方式去認為元素是什麼...亨廷頓公理系統來定義,但也有用比恩公理系統或具有0與1的有補分配格等來...分配格,如果我們對 a | b 寫 a ≤ b。這個格是布爾代數若且唯若n...
發現歷史 運算理論 衍生理論 套用領域圖書信息作者:Seymour Lipschutz著曹愛文等譯 圖書詳細信息:ISBN:9787302238508定價:69元印次...
圖書信息 圖書簡介 圖書前言 圖書目錄. *分配格, (L,*,°)是格,如果對"a,b,cÎL...)=(a°b)*(a°c) 則(L,*,°)為分配格. 滿足左、右分配律的格就是分配格. h格的運算性質(1) (L,£)是一個...
名詞解釋 詳情菱形格(diamond-type lattice ) 一類特殊的子格.典型的非分配格,但它是模格.格1.的子集A稱為菱形格若且唯若A是與M}同構的子格,其中M。如右圖所示.菱形格在分配格的刻畫中起重要作用. 菱形格 ...
