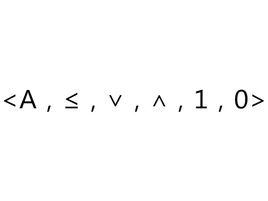基本介紹
布爾格是布爾代數的等價概念,布爾(G.Boole)研究命題演算時發現的,也是最早研究的格,有補的分配格稱為布爾格,若布爾格僅含一個元素,則稱為平凡布爾格,亨廷頓(E.V.Huntington)把布爾格表征為每一元a都有惟一的補元a′,且滿足(a∧b)′=a′∨b′和(a∨b)′=a′∧b′的格,若在布爾格(B;∧,∨)中把取補記成一元運算“′”,把0,1看做兩個零元運算,則(B;∧,∨)就成為布爾代數(B;∧,∨,′,0,1);反之,若在布爾代數中把二元運算∧,∨看成是格運算,把一元運算“′”看成是格中的元取補元時,它就成為布爾格.因而常把布爾格與布爾代數等同起來 。
定義
有補分配(complemented distributive)格定義
設<A,≤,∨,∧>是一個有界格,如果A既是有補格,又是分配格,那么A被稱為有補分配格 。
定理 設<A,≤,∨,∧>是一個有補分配格,A上每個元素都有唯一補元。
證明 有補格一定存在全上界1,和全下界0。有補格的每個元素至少有一個補元,因為格<A,≤,∨,∧>又是分配格,所以<A,≤,∨,∧>每個元素的補元唯一。
 布爾格
布爾格有補分配格上,每個元素的補元存在且唯一,此時元素x的補元可記為。
布爾格(Boolean lattice)定義
若<A,≤,∨,∧,1,0>是有補分配格,則稱其為布爾格。
布爾代數(Boolean algebra)定義
設<A,≤>是一布爾格,將對A上每個元素的求補看成一元補運算“﹣”,則布爾格可記為<A,≤,∨,∧,﹣,1,0>,並稱<A,∨,∧,﹣>為布爾代數。
原子(atom)定義
設<A,≤,∨,∧,1,0>是有界格,
A上蓋住全下界0的元素被稱為A上的原子。
A上被全上界1蓋住的元素被稱為A上的反原子。
布爾格是有界格,任何布爾格A,|A|>2。必存在正原子和反原子。一般稱正原子為原子。全上界1和全下界0不是原子 。
相關定理
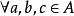 布爾格
布爾格定理1 設<A,≤,∨,∧,﹣>是任意布爾格,那么,
以下十大定律成立 :
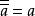 布爾格
布爾格對合律:
冪等律:a∨a=a
交換律:a∨b=b∨a
結合律:(a∨b)∨c=a∨(b∨c)
分配律:a∨(b∧c)=(a∨b)∧(a∨c)
吸收律:a∧(a∨b)=a
同一律:a∨0=a
零律:a∨1=1
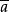 布爾格
布爾格互補律:a∨=1
 布爾格
布爾格De.Morgan律:
定理2 設<A,≤,∨,∧,﹣>是一布爾格,任意原子a∈A,與另一個非零元素b∈A之間,必有且僅有a≤b或a≤6兩者之一成立 。
定理3 設<A,≤,∨,∧,﹣>是一有限布爾格,b∈A是任意一個非0元素,至少存在一個原子a∈A,使a與b同在一條鏈上 。