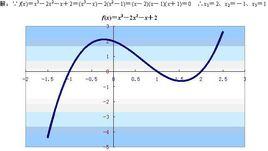
含義
一般地,對於函式y=f(x)(x∈R),我們把方程f(x)=0的實數根x叫作函式y=f(x)(x∈R)的零點(the zero of the function)。即函式的零點就是使函式值為0的自變數的值。函式的零點不是一個點,而是一個實數。
術語解釋
使得某系統的傳遞函式G(s)為0的s的值(注意s為複數),該值在複平面上的點,就是零點。
若該系統的輸入為U(s),當s取值為零點處的值,則G(s)=0。又因為系統輸出Y(s)=G(s)·U(s),而s的特殊取值使得G(s)=0,所以此時無論輸入信號為何種形式,最終輸出Y(s)都是0,這也是 零點的實際意義。
也可以這樣說,若某系統工作在零點上,那么此時任何輸入經過該系統後,輸出都是0。
一般結論
若函式y=f(x)在閉區間[a,b]上的圖像是連續曲線,並且在區間端點的函式值符號不同,即f(a)·f(b)≤0,則在區間[a,b]內,函式y=f(x)至少有一個零點,即相應的方程f(x)=0在區間[a,b]內至少有一個實數解。
一般結論:函式y=f(x)的零點就是方程f(x)=0的實數根,也就是函式y=f(x)的圖像與x軸(直線y=0)交點的橫坐標,所以方程f(x)=0有實數根,推出函式y=f(x)的圖像與x軸有交點,推出函式y=f(x)有零點。
更一般的結論:函式F(x)=f(x)-g(x)的零點就是方程f(x)=g(x)的實數根,也就是函式y=f(x)的圖像與函式y=g(x)的圖像交點的橫坐標,這個結論很有用。
變號零點就是函式圖像穿過那個點,也就是在那個點兩側取值是異號(那個點函式值為零)。
不變號零點就是函式圖像不穿過那個點,也就是在那個點兩側取值是同號(那個點函式值為零)。
注意:如果函式最值為0,則不能用此方法求零點所在區間。
套用
二分法求方程的近似解
(1)確定區間[a,b],驗證f(a)f(b)<0,給定精確度;
(2)求區間(a,b)的中點x;
(3)計算f(x);
①若f(x1)=0,則x就是函式的零點;
②若f(a)f(x)<0,則令b=x(此時零點x∈(a,x1));即圖象為(a,x)
③若f(x)f(b)<0,則令a=x。(此時零點x∈(x,b)
(4)判斷是否滿足條件,否則重複(2)~(4)