函式定義
 L-函式
L-函式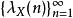 L-函式
L-函式一般地, 對於數學對象, 我們可定義複數列, 形如
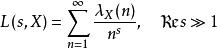 L-函式
L-函式 L-函式
L-函式 L-函式
L-函式且具有Euler乘積的Dirichlet級數, 我們稱其為關於的-函式。
函式來源
 L-函式
L-函式一般地說,-函式來源由兩類組成: 算術L-函式和自守L-函式. 這兩者又是密切聯繫在一起的, 根據羅伯特·朗蘭茲的猜想, 籠統地說, 一切有意義的L-函式都來自自守L-函式.
算術L-函式
簡單地說,
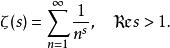 L-函式
L-函式同樣地,狄利克雷在研究算術級數中的素數分布時,引入了Dirichlet L-函式:
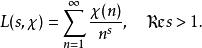 L-函式
L-函式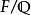 L-函式
L-函式Dedekind zeta-函式: 設為一代數數域,
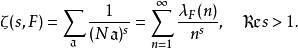 L-函式
L-函式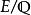 L-函式
L-函式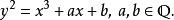 L-函式
L-函式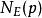 L-函式
L-函式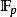 L-函式
L-函式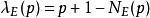 L-函式
L-函式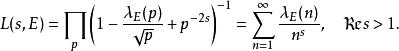 L-函式
L-函式橢圓曲線的Haass-Weil L-函式: 設為一非奇異的橢圓曲線定義為曲線在有限域上的解, 設, 則下面的級數稱為關於曲線的Haass-Weil L-函式
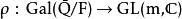 L-函式
L-函式 L-函式
L-函式阿廷L-函式: 設是一個有限維的伽羅瓦表示,其中為一代數數域,
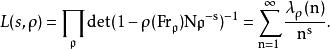 L-函式
L-函式自守L-函式
全純模形式的L-函式, Maass L-函式, 標準L-函式等等 .
研究內容
根據羅伯特·朗蘭茲在國際數學家大會上的報告所指, 研究一個L-函式主要有三部分內容 :
解析延拓
L-函式的解析延拓和函式方程這是最基本的一部分. 對於一般的自守L-函式這是較容易得到的, 但是對算術的L-函式這一部分並不是容易得到的. 例如, 對於Haass-Weil L-函式, 這部分就是谷山-志村猜想, 該猜想一部分就能推出費爾馬大定理. 關於阿廷L-函式的全純解析沿拓的阿廷猜想也是數論中重要的未知問題.
 L-函式
L-函式對於數學對象的L-函式, 我們定義其的gamma因子為
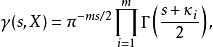 L-函式
L-函式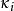 L-函式
L-函式其中為復參數.
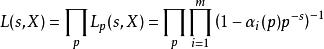 L-函式
L-函式 L-函式
L-函式 L-函式
L-函式定義下面關於的完全-函式
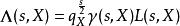 L-函式
L-函式那么, 一般地我們有函式方程
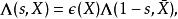 L-函式
L-函式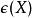 L-函式
L-函式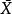 L-函式
L-函式 L-函式
L-函式其中為模為1的複數,為關於的對偶對象.
零點的分布
非零區域: 如黎曼zeta函式的目前最好的非零區域為
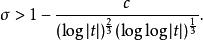 L-函式
L-函式黎曼猜想和廣義黎曼猜想問題 :
在假設黎曼猜想下, 零點虛部的分布問題與隨機矩陣的聯繫等等.
特殊點的值
中心值, 臨界點, 整點的值, 極點的留數等. 這裡面也有很多猜想, 像BSD猜想, 類數問題, Deligne 猜想,Beilinson 猜想,Goldfeld猜想. 其實往往我們重要的不僅是關心它具體有多大,而是關心的這個量裡面隱含著什麼樣的算術意義。像Dedekind zeta 函式在s=1處的留數,裡面包含了一個數域的很多不變數:類數,判別式,regular等;BSD猜想就是Haass-Weil L-函式在中心點的的階就是該橢圓曲線的秩!
研究意義
 L-函式
L-函式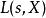 L-函式
L-函式 L-函式
L-函式對於一個研究對象如素數, 伽羅瓦擴張, 橢圓曲線, 代數簇等等, 我們可根據其性質構造出一個復變數的L-函式. -函式的解析性質: 零點和極點, 函式方程, 展開係數, 特殊點的值等等, 往往能夠充分反映的算術, 幾何, 或代數性質.
三個公開問題
關於L-函式的研究,有許多未解決的公開問題,在這些問題中,尤以下面三個著名 .
廣義Riemann猜想
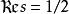 L-函式
L-函式L-函式所有非平凡的零點均位於線上.
廣義Lindelof猜想
在(3.1)的函式方程中, 有猜想:
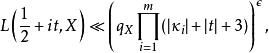 L-函式
L-函式 L-函式
L-函式其中為任意小的正實數.
廣義Ramanujan猜想
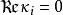 L-函式
L-函式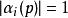 L-函式
L-函式在(3.1)的函式方程中,猜想對非分歧的有和.
