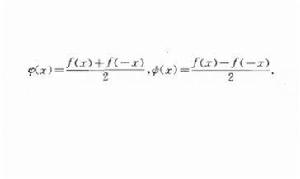 函式的奇偶性
函式的奇偶性函式的奇偶性(odevity of a function),對任意xEl,若f(-x)=f(x),即在關於y軸的對稱點的函式值相等,則f(x)稱為偶函式;若f(-x)= - f(x),即對稱點的函式值正負相反,則f(x)稱為奇函式.在平面直角坐標系中,偶函式的圖象對稱於y軸,奇函式的圖象對稱於原點.可導的奇(偶)函式的導函式的奇偶性與原來函式相反.定義在對稱區間(或點集)上的任何函式f(x)都可以表示成奇函式φ( x)和偶函式ψ(x)之和。
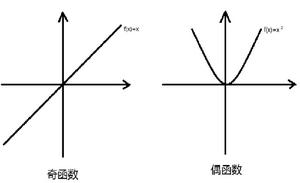
函式的奇偶性是指在關於原點的對稱點的函式值相等。是函式的基本性質之一,指其圖象有某種對稱性的一元函式.定義在對稱區間1= (-a,a)或[-a,a}(或數軸上關於原點對稱的點集)上的(一元)實值函式y=f (x)。
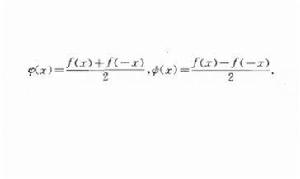 函式的奇偶性
函式的奇偶性函式的奇偶性(odevity of a function),對任意xEl,若f(-x)=f(x),即在關於y軸的對稱點的函式值相等,則f(x)稱為偶函式;若f(-x)= - f(x),即對稱點的函式值正負相反,則f(x)稱為奇函式.在平面直角坐標系中,偶函式的圖象對稱於y軸,奇函式的圖象對稱於原點.可導的奇(偶)函式的導函式的奇偶性與原來函式相反.定義在對稱區間(或點集)上的任何函式f(x)都可以表示成奇函式φ( x)和偶函式ψ(x)之和。
奇函式在其對稱區間[a,b]和[-b,-a]上具有相同的單調性,即已知是奇函式,它在區間[a,b]上是增函式(減函式),則在區間[-b,-a]上也是增函...
定義 特徵 證明方法 性質 要點詮釋奇偶性是函式的基本性質之一。一般地,如果對於函式f(x)的定義域內任意一個x,都有f(-x)=f(x),那么函式f(x)就叫偶函式。一般地,如果對於函式...
定義 圖像特徵 運算 判斷單調 誤區警示函式的定義:給定一個數集A,假設其中的元素為x。現對A中的元素x施加對應法則f,記作f(x),得到另一數集B。假設B中的元素為y。則y與x之間的等量關係...
詳細介紹 發展歷史 函式定義 表示方法 函式的特性函式(function)表示每個輸入值對應唯一輸出值的一種對應關係。函式f中對應輸入值的輸出值x的標準符號為f(x)。包含某個函式所有的輸入值的集合被稱...
頂點式 三角函式 最值問題 學習指導分段函式,就是對於自變數x的不同的取值範圍,有著不同的解析式的函式。它是一個函式,而不是幾個函式;分段函式的定義域是各段函式定義域的並集,值域也是各段函...
函式類型 例子 分段函式題型二次函式(quadratic function)的基本表示形式為y=ax²+bx+c(a≠0)。二次函式最高次必須為二次, 二次函式的圖像是一條對稱軸與...
基本定義 歷史 函式性質 表達式 函式圖像初等函式是由基本初等函式經過有限次的四則運算和複合運算所得到的函式。基本初等函式和初等函式在其定義區間內均為連續函式。不是初等函式的函式,稱為非初等函式...
分類方法 冪函式 指數函式 對數函式 三角函式0)的函式。由圖像得名,又被稱為“雙勾函式”、“勾函式”、"對號函式"、“雙飛燕函式”等。因函式圖像和耐克商標相似,也被形象稱為“耐克函式”或“耐克曲線”。
函式定義 性質 均值不等式 導數求解 其它解法我們把沒有給出具體解析式的函式稱為抽象函式。由於這類問題可以全面考查學生對函式概念和性質的理解,同時抽象函式問題又將函式的定義域,值域,單調性,奇偶性,...
函式介紹 微分方程 學好函式 解法舉例