六角幻方

六角幻方或六邊幻方也叫蜂巢幻方，它是由美國人阿當斯研究出來的，由正六邊型組成的幻方。六角幻方是由從1到19的19個自然數組成，它的每一行、每一斜的數字都等於38，它具有三、四、五、六、七、八數幻和。理論上只有一種解法。

基本信息

• 中文名：六角幻方
• 英文名：Magic hexagon

• 發現者：阿當斯
• 特徵：六邊型組成的幻方

研究過程

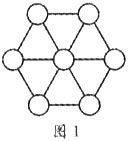一層六角幻方

1910年，一位名叫阿當斯的鐵路公司閱覽室青年職員，對六角幻方很感興趣。他知道一層六角幻方(把1到7這7個數填入（如圖1）所示的圓圈內，使得任一條直線上的數字之和都等於同一個數)根本不存在，因而把注意力集中在由19個數組成的兩層六角幻方上。

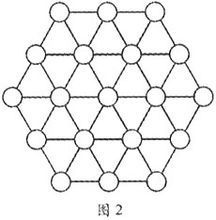二層六角幻方

他一有空閒時間，便在紙上或地上畫兩層六角圖（如圖2），再把19塊上面寫有1到19這19個數的硬紙板在圖上擺來擺去就這樣，一天又一天，一年又一年，漫漫的47個春秋過去了，這時的阿當斯已不再是當年英俊瀟灑的小伙子，無情的歲月，使他成了兩鬢斑白的老人.面對無數次的失敗與挫折，阿當斯的興趣依然不減。

結果

“皇天不負苦心人”，1957年的一天，患病在床的阿當斯終於排列成功了。他驚喜萬分，連忙找紙把它記錄下來，不幸的是，當他病癒出院回到家中時，卻發現那張記錄六角幻方的紙卻不見了。阿當斯並不因此灰心喪氣，恰恰相反，他又奮鬥了5年。終於在1962年12月的一天，重新找到了那個丟失的圖形.這個圖形有個奇特的性質，就是橫的五行及斜的十行上各自數字的和都是38。

阿當斯對於耗費自己畢生心血而得來的六角幻方視如珍寶，並把它拿給幻方專家馬丁·加德納鑑賞。面對這巧奪天工的珍寶，馬丁·加德納博士頓感眼界大開，並為此寫信給智慧超群的數學遊戲專家特里格.特里格驚奇萬分並深受鼓舞，決心在阿當斯六角幻方的基礎上，對層數作出突破。他經過反覆研究，終於驚奇地發現：兩層以上的六角幻方根本不存在。這就是說，普通的幻方可能有千千萬萬種排法，但六角幻方卻只能有阿當斯這一個。

1969年，滑鐵盧大學二年級學生阿萊爾對特里格的結論作了簡單而又巧妙的證明.阿萊爾並不以此為滿足，他又把六角幻方的可能選擇輸入電子計算機測試，結果用了17秒時間，得出了與阿當斯完全相同的結果。面對著47年與17秒的懸殊，同學們在讚嘆阿當斯堅持不懈的研究精神的同時，更應該發憤努力學習，以期掌握當今世界最新的科學技術。