分析法
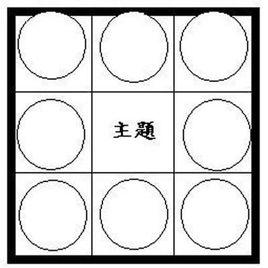
（一）曼陀羅法
曼陀羅法是一種有助擴散性思維的思考策略，利用一幅像九宮格圖，將主題寫在中央，然後把由主題所引發的各種想法或聯想寫在其餘的八個圈內，此法也可配合六何法從多方面進行思考。
[備註]：此九宮格法可作為擴散性思維的基本單位，由此演變出其它九宮格法（如蓮花法中央的單位，正是曼陀羅法的基本單位）。此法之優點乃由事物之核心出發，向八個方向去思巧，發揮八種不同的創見。而蓮花法也是依循此思維方式加以發揮並擴散其思考範圍。
（二）蓮花法
這是從曼陀羅法的基本單位發展擴展而來（下圖）。
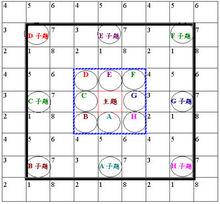蓮花法(1) 每位討論者手持一蓮花圖，並將討論之主題或問題寫於圖中央位置。
(2) 把相關的意念寫於圍著主題四周的八個圈中（每個圈的左上角分別寫上英文字母A至H），成為八個子題，並於圖中央部分構成了一幅曼陀羅法九宮圖。隨後，討論者可就各個子題再想出另外八個意念，將之寫於圍著「子題」四周及標著1-8號碼的方格內，討論者可沿以上步驟再延伸構思新的意念。
(3) 討論直至整個蓮花圖寫滿為止。
概說
（1）起源
目前普遍認為，九宮數圖即為“洛書”的主要內容，是最早關於數的起源之說（見圖3）。《周易·繫辭上》說：“河出圖，洛出書，聖人則之。”但其中並沒有明確記載“洛書”的主要內容。直至西漢經學家孔安國的《尚書·洪範傳》才提到：“天與禹，洛出書。神龜負文而出列於背，皆有數至於九。禹遂因而第之，以成九類，常道所以次序。” 劉歆注1云：“伏羲氏繼天而王，受河圖而畫之，八卦是也。禹治洪水，賜洛書，法而陳之，九疇是也。” 其九疇，即“戴九履一，左三右七，二四為肩，六八為足，五居中央，正龜背之象也”。
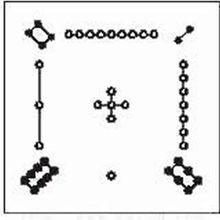《周易本經》的洛書圖解據《史記·夏本紀》記載：夏禹治水時，“左準通，右規矩，載四時，以開九州，通九道，陳九澤……”。此後大禹以洛書為據，套用到測量、氣象、地理與交通運輸之中，從而治理黃河，大獲成功。由於神龜所背圖是在黃河支流洛水中發現，且圖中內容如書一樣深奧，故稱之為洛書。
而九宮之說首見於《大戴禮記·明堂篇》，其中言到，明堂有“九室”(見下圖)，其形上圓下方，其數為：“二四九，七五三，六一八。”其中所記載的九疇、祠廟、太廟、明堂等建築都用此方法。之後，九宮結構多被用於皇帝的宮室中。《管子·幼官》、《呂氏春秋·十二紀》、《禮記·月令》等典籍中都有關於天子在一年四季分居九個不同宮室的記載。
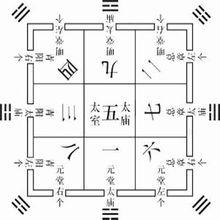明堂九室圖後人根據九宮數圖創造了“九宮算”的計算方法，我國後漢徐岳的《數術記遺》一書中已有記載：“九宮算注2, 五行參數, 猶如循環, 九宮者, 即二四為肩, 六八為足, 左三右七, 戴九履一, 五居中央。”[4]
（2）排列規律
九宮數圖既是一種組合計算，又是一種益智遊戲。後來形成的“九宮算”及“排九宮”等都是以九宮數圖為基礎（見下圖）。
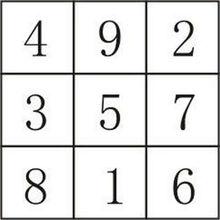九宮數圖九宮數圖最基本的規律，是其縱橫及對角線上三數之和都為15，且九個數相加之和為45，是15的3倍。深入研究其數字的排列組合，可以發現以下規律：
①其8組數列中包含4組等差數列：[4、5、6] 、[3、5、7]、 [8、5、2] 、[1、5、9]，以5為中心，逆時針方向，各數列的公差分別為1、2、3、4，又是一個以1為公差的等差數列（如下圖所示）；
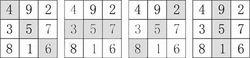九宮圖分析法②另四組數列也有一定的規律（如下圖所示），從圖中可以看出，這四個數列相鄰兩數的差顛倒對稱，而且四邊的數中，均有相鄰兩數之差為5，且各個數字均不重複，具體為：上[4、9、2]9-4=5；下[8、1、6]6-1=5；左[4、3、8]8-3=5；右[2、7、6]7-2=5；
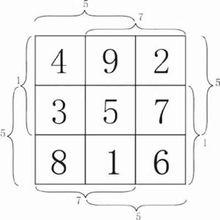九宮數圖③奇數和偶數相互交錯排列，四角之數為偶數，中間之數為奇數，同時，中間除5之外的四個數，任何兩個之差都為偶數，且分別為四角四個數，具體為：9-7=3-1=2；9-3=7-1=6；9-1=8；7-3=4（如下圖所示）。
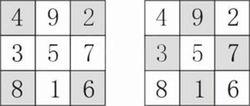九宮數圖注釋
·注1：孔安國：字子國，孔子十一代孫，西漢經學家；劉歆：字子發，漢宗室劉向之子，對於數術方技頗有研究，為中國研究求圓周率之第一人。
·注2：“九宮算”是指以九宮數圖為基礎的計算方法，是指世界上最早出現的數學智力遊戲,後來發展到“排九宮”，就是人們將9 塊分別寫有自然數1—9的正方形棋子在九宮格中布陣來構造三階幻方,是世界上最早出現的幾何形塊的玩具。
參考文獻
1.蘇勇點校，易經，北京大學出版社，1989，第85頁。
2.朱熹，周易本義，北京大學出版社，1992，第147，207頁。
3.林忠軍，試論鄭玄易數哲學，孔子研究，2003.3。
4.康小虎，論九宮圖與古代計算法的關係，延安教育學院學報，2001.4。
