三角形ABC的BC邊上有一點P,則可滿足下列關係:
 斯德瓦特定理
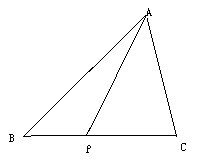
斯德瓦特定理證明如下:如圖:
∵∠APB+∠APC=180°
∴cos∠APB=-cos∠APC
由余弦定理可知:cos∠APB=(AP^2+BP^2-AB^2)/(2*BP*PC)
cos∠APC=(AP^2+PC^2-AC^2)/(2*AP*PC)
將上面兩個式子代入可得到:
(AP^2+BP^2-AB^2)/(2*BP*PC)=-(AP^2+PC^2-AC^2)/(2*AP*PC)
將上述式子整理可得到:
AB^2*PC+AC^2*BP=AP^2*(BP+PC)+BP*PC*(BP+PC)
由圖可知:BP+PC=BC,代入即得到:
AB^2*PC+AC^2*BP=AP^2*BC+BP*PC*BC
