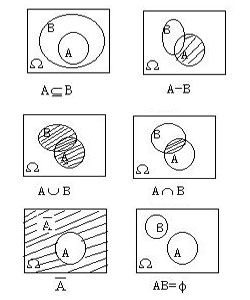
定義
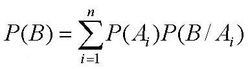
若事件A1,A2,…構成一個完備事件組且都有正機率,則對任意一個事件B,有如下公式成立:
此公式即為全機率公式。
特別地,對於若事任意兩事件A和B,有如下成立:
P(B)=P(B|A)P(A)+P(B|Ac)P(Ac)
其中A和Ac為互補事件。
套用舉例
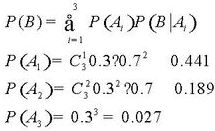 全機率公式計算
全機率公式計算例:高射炮向敵機發射三發炮彈,每彈擊中與否相互獨立且每發炮彈擊中的機率均為0.3,又知敵機若中一彈,墜毀的機率為0.2,若中兩彈,墜毀的機率為0.6,若中三彈,敵機必墜毀。求敵機墜毀的機率。
解:設事件B=“敵機墜毀”;Ai=“敵機中 彈”;i=0,1,2,3
實際上我們從題目知道應該是A0,A1,A2,A3構成完備事件組,但是敵機墜毀只和A1,A2,A3有關,即 ,則我們可用如下公式
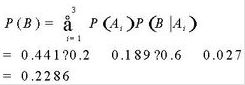 全機率公式計算
全機率公式計算