機率的加法法則
定理:設 A 、 B是 互不相容事件(AB=φ),則:
P ( A ∪ B ) =P ( A ) +P ( B )
推論1:設A1、 A2、…、 An互不相容,則: P(A1+A2+...+ An)= P(A1) +P(A2) +…+ P(An)
推論2:設A1、 A2、…、 An構成完備事件組,則: P(A1+A2+...+An)=1
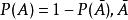 機率計算
機率計算推論3:為事件 A的對立事件。
推論4:若B包含A,則 P(B-A)= P(B)-P(A)
推論5(廣義加法公式):
對 任意兩個事件 A 與 B,有 P(A ∪ B)=P(A)+P(B) - P(AB)
條件機率
條件機率:已知事件B出現的條件下A出現的機率,稱為條件機率,記作:P(A|B)
條件機率計算公式:
當P(A)>0,P(B|A)=P(AB)/P(A)
當P(B)>0,P(A|B)=P(AB)/P(B)
乘法公式
P(AB)= P(A) × P(B|A) =P(B) ×P(A|B)
推廣:P(ABC)=P(A)P(B|A)P(C|AB)
全機率公式
設:若事件A1,A2,…,An互不相容,且A1+A2+…+An=Ω,則稱A1,A2,…,An構成一個完備事件組。
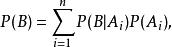 機率計算
機率計算全機率公式的形式如下:
以上公式就被稱為全機率公式。
例題
一個20面體,每個面都是等邊三角形,如果截去所有的頂角,它將成為多少面體?共有多少個頂點?共有多少條棱?
| 面體 | 頂點 | 條棱 |
| 4 | 2*(4-2)=4 | 3*(4-2)=6 |
| 5 | 2*(5-2)=6 | 3*(5-2)=9 |
| 6 | 2*(6-2)=8 | 3*(6-2)=12 |
| 7 | 2*(7-2)=10 | 3*(7-2)=15 |
| 8 | 2*(8-2)=12 | 3*(8-2)=18 |
| n | 2*(n-2) | 3*(n-2) |
| 20 | 2*(20-2)=36 | 3*(20-2)=54 |
每截去一個頂角(頂角數量=頂點數量),增加一個面;
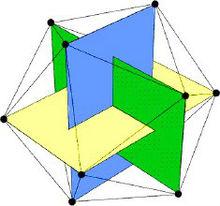 20面體
20面體一個20面體截去所有頂角(頂角數量=頂點數量),即增加36個面;
| 面體 | 頂點 | 條棱 |
| 20+36=56 | 2*(56-2)=108 | 3*(56-2)=162 |

