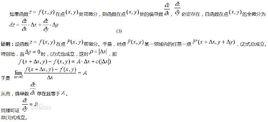全增量
為了引進全微分的定義，先來介紹全增量。
設二元函式z = f (x, y)在點P(x,y)的某鄰域內有定義，當變數x、y點(x,y)處分別有增量Δx，Δy時函式取得的增量。
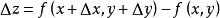全微分稱為 f (x, y)在點(x,y)的全增量。
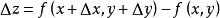全微分
全微分如果函式z = f (x, y)在點(x,y)的全增量 可表示為
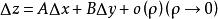全微分
全微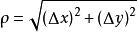分
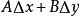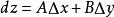全微分
全微分其中A 、B僅與x、y 有關，而不依賴於Δx 、Δy， ，則稱函式z = f (x, y)在點(x,y)處可微分， 稱為函式z = f (x, y)在點(x,y)處的全微分。記作dz，即。
函式若在某平面區域D內處處可微時，則稱這個函式是D內的可微函式，全微分的定義可推廣到三元及三元以上函式。
定理
定理1
如果函式z=f（x，y）在點p（x0，y0）處可微，則z=f（x，y）在p（x0，y0)處連續，且各個偏導數存在，並且有f′x（x0，y0）=A，f′y（x0，y0）=B。
定理2
若函式z=f（x，y）在點p0（x0，y0）處的偏導數f′x，f′y連續，則函式f在點p處可微。
定理3
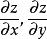全微分若函式z = f (x, y)在點(x, y)可微分，則該函式在點(x,y)的偏導數必存在，且函式z = f (x, y)在點(x,y)的全微分為：
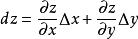全微分判別可微方法
(1)若f (x,y)在點(x0, y0)不連續，或偏導不存在，則必不可微；
(2)若f (x,y)在點(x0, y0)的鄰域內偏導存在且連續必可微；
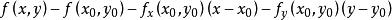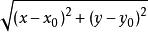全微分
全微分(3)檢查是否為的高階無窮小，若是則可微，否則不可微。
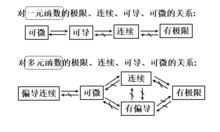
極限、連續、可導、可微的關係
全微分這幾個概念之間的關係可以用下圖表示：
