基本概念
微分運算是一種基本的數學運算，在信號分析與處理等領域得到廣泛套用，特別在信號的奇異性檢測和提取方面具有特殊的作用。我們常用的微分運算，微分方程等使用的都是整數階，例如一階導數、二階導數⋯，一階微分方程、二階微分方程⋯，然而許多事物、自然現象以及社會現象，例如諸多“非”問題和現象是難以用整數階微分方程來描述和刻畫的。從信號分析與處理角度來看，微分運算，即對函式或信號f(t)求導：
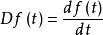數字微分器數字微分器，是指執行微分運算的數字方式。整數階數字微分器用於確定和估計給定信號的（一般是關於時間）導數是十分有用的工具。例如，在雷達和聲納套用中，速度和加速度是用微分器從位置測量數據計算出來的。在生物醫學工程中，通常需要獲得生物醫學數據中，特別是在低頻區間的高階導數。對於整數階，也即普通微分濾波器的設計理論己很成熟並得到廣泛套用。
理想數字微分器設計
定義
從信號處理角度來看，整數階或分數階（階數為v）微積分運算完全可以看成是對信號的濾波，濾波函式即是
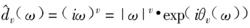數字微分器有如下三種情況：
（1）v>0，對應於微分函式
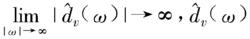數字微分器是奇異高通濾波；
（2）v=0，對應於全通函式
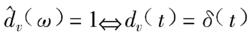數字微分器（3）v<0，對應於積分函式
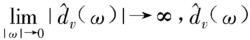數字微分器是奇異低通濾波。
根據數位訊號處理理論，我們將理想的數字分數階微分濾波函式定義為：
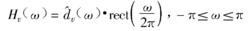數字微分器性質
這樣得到的理想數字分數微分濾波器，滿足如下基本性質：
（1）有界性
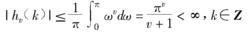數字微分器（2）波動性
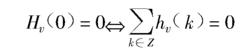數字微分器（3）實值性
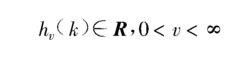數字微分器（4）連續性
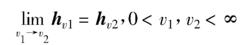數字微分器（5）能量有限性
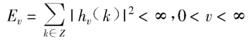數字微分器一階微分器
微分運算是許多物理系統和計算系統中常用的基本手段，微分器在測試技術、控制工程及生物工程中得到了廣泛的套用。但是對連續信號或離散信號求導數，通常是一個不穩定的過程。
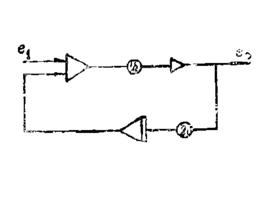
下面介紹一種直接從被測信號中得到低階，又能抑制噪聲的微分器。模擬電路為 ：
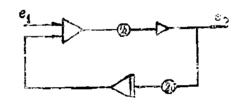數字微分器可以得到積分方程為：
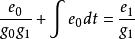數字微分器經拉氏變換得：
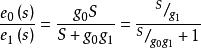數字微分器下圖是框圖：
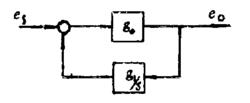數字微分器波特圖為：
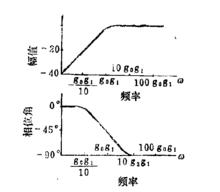數字微分器這是包含了一階低通濾波器的微分器。
數字微分器的Matlab實現
測試數據進行微分和積分計算是經常遇到的問題，對於有解析表達式的函式，求其微分往往比積分容易得多。但對由測量系統測得的數據進行微分和積分情況就不一樣了，為滿足一定的工程計算精度，進行微分計算常比積分困難得多。目前，常用的微分方法有兩種：用模擬微分器進行實時微分獲取，用軟體設計數字微分器對已測得的數據進行微分處理。
Matlab語言是一種面向科學與工程計算的語言，高版本的Matlab語言有豐富的庫函式，用戶檔案也可作為Matlab的庫函式直接調用。用戶可以根據自己的需要方便地建立和擴充新的庫函式。充分利用Matlab語言的函式功能，可以完成數字微分器的程式設計，並將其作為函式檔案保存，可方便地進行調用。
原始數據的獲取
測試數據為某一運動物體的速度，感應測速感測器的工作原理是：當物體運動時，帶動與其固聯的永久磁鐵沿速度線圈軸線方向運動，通過電磁感應原理把物體的運動速度變換成和它保持一定比例關係的感應電動勢。測量放大器的功能是放大感測器的輸出信號，並改善整個測量系統的動態回響.速度信號含有豐富的高頻成分，採用模擬微分器需要嚴格調節微分器的時間常數等，微分的效果不理想，因此設計數字微分器對速度信號進行微分處理以獲得其加速度信號。系統框圖如下：
數字微分器數字微分器設計
設計數字微分器的理論依據是模擬微分器的頻率回響函式.模擬微分器的頻率回響函式為：
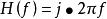數字微分器其衝擊回響函式為：
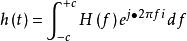數字微分器計算實例
Matlab程式如下：
function a=dif(v,Ts,ft,N,M0,N1)/可供調用的微分子函式/
kd=2*ft*Ts;
h(M0+1)=0;
pai=3.14;
for i=0:M0-1
B=pai*kd*(i-M0);
h1=1-cos(pai*i/M0);
h2=B*cos(B)-sin(B);
h(i+1)=h2/(2*pai*Ts)*h1/(i-M0)^2;
end;
for i=M0+1:2*M0-1
B=pai*kd*(i-M0);
h1=1-cos(pai*i/M0);
h2=B*cos(B)-sin(B);
h(i+1)=h2/(2*pai*Ts)*h1/(i-M0)^2;
end;/計算數字微分器的衝擊回響/
V=fft(v,N);
H=fft(h,N)；
Z=V*H;
z=ifft(Z);
a=real(z);/利用Matlab的函式做兩次FFT和一次IFFT/
for i=0:N1-1
a(i+1)=a(i+1+M0);
end;
for
i=N1:N1-1+2*M0-1
a(i+1)=0;
end;/將序列向右平移M0/
