數值微分
正文
根據函式在一些離散點的函式值，推算它在某點的導數或某高階導數的近似值。通常用差商代替微商，或用一能近似代替該函式的較簡單的函式（如多項式、樣條函式）的相應導數作為所求導數的近似值。例如，對帶餘項的插值公式ƒ(x)=I(x)+R(x)取k階導數就得到帶餘項的數值微分公式
,這裡插值函式I(x)的k階導數I(k)(x)即為所求k階導數 ƒ(k)(x)的近似值，而插值函式餘項R(x)的k階導數R(k)(x)則給出此近似值的截斷誤差。 通常利用多項式插值進行數值微分。設函式ƒ(x)在n+1個等距點xv=α+vh（v=0,1,…,n）上的值ƒv=ƒ(xv)為已知，則通過低次插值可導出一些最基本和常用的數值微分公式，例如，兩點公式
三點公式
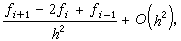等等。此外,利用具有n+1個等距節點的拉格朗日插值公式,還可導出在節點xj(i=0,1,…,n)上的較為一般的數值微分公式 
式中
因此，當節點的個數n+1固定時，間距h愈小，則截斷誤差也愈小。但是這時係數絕對值之和
隨h的變小而劇增,所以函式值ƒv的捨入誤差對近似導數的影響也隨h的變小而劇增。因此，h並非愈小愈好，而是要適中，這是數值微分不同於某些插值之處。如果函式ƒ(x)有很好的可微性，即存在絕對值不太大的較高階導數，則寧取間距稍大而個數稍多的節點。當ƒ(x)在節點分布的整個區間上的可微性不太好時，利用樣條插值進行數值微分比利用多項式插值更適宜，只是計算量要大得多。 如果數據ƒv帶有不容忽視的隨機誤差，而其對應的自變數分布甚密，就應該用曲線擬合代替上述函式插值，然後用擬合曲線的導數作為函式ƒ(x)的導數的近似值。這樣求得的導數叫做磨光的導數。
參考書目
馮康等編：《數值計算方法》，國防工業出版社，北京，1978。
