分類
 阿貝爾微分
阿貝爾微分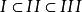 阿貝爾微分
阿貝爾微分設 g 是曲面 S 的虧格; 是 S 的典範同調基的閉鏈,根據它們奇點的性狀,將它們分成三類阿貝爾微分:Ⅰ,Ⅱ和Ⅲ ,並且有真包含關係 。
第一類阿貝爾微分
(Abelian differential of the first kind)
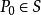 阿貝爾微分
阿貝爾微分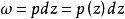 阿貝爾微分
阿貝爾微分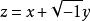 阿貝爾微分
阿貝爾微分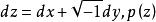 阿貝爾微分
阿貝爾微分第一類阿貝爾微分就是 S 上處處全純的一階微分,且在每個點 的一個鄰域 U 內它具有形式 ,這裡 是 U 內的局部單值化變數, 是 U 內 z 的全純或正則的解析函式。
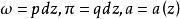 阿貝爾微分
阿貝爾微分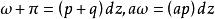 阿貝爾微分
阿貝爾微分 阿貝爾微分
阿貝爾微分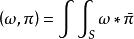 阿貝爾微分
阿貝爾微分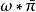 阿貝爾微分
阿貝爾微分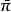 阿貝爾微分
阿貝爾微分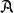 阿貝爾微分
阿貝爾微分阿貝爾微分相加或它與一個全純函式相乘可以用自然的方式:如果 ,則 。第一類阿貝爾微分構成一個 g 維的向量空間 。再引入標量積 ,其中 是與星共軛微分 的外積 (exterior product),空間 成為希爾伯特空間。
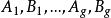 阿貝爾微分
阿貝爾微分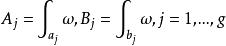 阿貝爾微分
阿貝爾微分設 是第一類阿貝爾微分ω的 A 周期和 B 周期,即積分 。那那么有以下關係式:
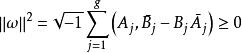 阿貝爾微分
阿貝爾微分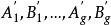 阿貝爾微分
阿貝爾微分 阿貝爾微分
阿貝爾微分如果 是另一個第一類阿貝爾微分 的周期,那么有
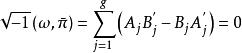 阿貝爾微分
阿貝爾微分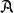 阿貝爾微分
阿貝爾微分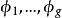 阿貝爾微分
阿貝爾微分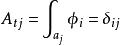 阿貝爾微分
阿貝爾微分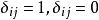 阿貝爾微分
阿貝爾微分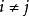 阿貝爾微分
阿貝爾微分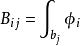 阿貝爾微分
阿貝爾微分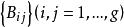 阿貝爾微分
阿貝爾微分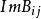 阿貝爾微分
阿貝爾微分 阿貝爾微分
阿貝爾微分關係式(1)和(2)稱為第一類阿貝爾微分的黎曼雙線性關係 (bilinear Rienmann relations)。可以選取第一類阿貝爾微分的一個典範基,即空間 的一個典範基 ,使得 ,這裡 ,若 。於是 B 周期 矩陣 是對稱的,而且虛部的矩陣 是正定的。A 周期全為零或 B 周期全為零的第一類阿貝爾微分 的所有周期全為實數,那么ω=0 。
第二類和第三類阿貝尓微分
(Abelian differentials of the second and third kinds)
第二類和第三類阿貝爾微分通常是亞純微分,即在 S 上至多只有有限多個奇點(為極點)的解析微分,它們有局部表達式:
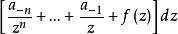 阿貝爾微分
阿貝爾微分 阿貝爾微分
阿貝爾微分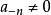 阿貝爾微分
阿貝爾微分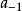 阿貝爾微分
阿貝爾微分 阿貝爾微分
阿貝爾微分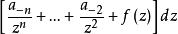 阿貝爾微分
阿貝爾微分其中 是正則函式,n 是極點的階(若 ),且 是極點的留數。如果 ,這個極點稱為單的。第二類阿貝爾微分就是所有留數都為零的亞純微分,即具有局部表達式 的亞純微分。第三類阿貝爾微分是一個任意的阿貝尓微分。
 阿貝爾微分
阿貝爾微分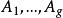 阿貝爾微分
阿貝爾微分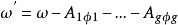 阿貝爾微分
阿貝爾微分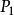 阿貝爾微分
阿貝爾微分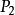 阿貝爾微分
阿貝爾微分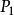 阿貝爾微分
阿貝爾微分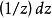 阿貝爾微分
阿貝爾微分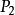 阿貝爾微分
阿貝爾微分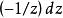 阿貝爾微分
阿貝爾微分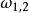 阿貝爾微分
阿貝爾微分 阿貝爾微分
阿貝爾微分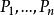 阿貝爾微分
阿貝爾微分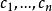 阿貝爾微分
阿貝爾微分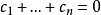 阿貝爾微分
阿貝爾微分 阿貝爾微分
阿貝爾微分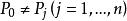 阿貝爾微分
阿貝爾微分 阿貝爾微分
阿貝爾微分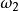 阿貝爾微分
阿貝爾微分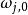 阿貝爾微分
阿貝爾微分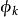 阿貝爾微分
阿貝爾微分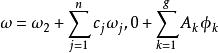 阿貝爾微分
阿貝爾微分設 是具有 A 周期 的一個任意阿貝尓微分;那么阿貝爾微分 的 A 周期都是零,稱為 正規阿貝爾微分(mormlized Abelian differential) 。特別地,當 和 是 S 上任意兩點時,可以構造一個在 有奇點 ,在 有奇點 的正規化阿貝爾微分 是第三類正規阿貝爾微分。設是任意阿貝爾微分,它在點 處分別有留數 ;那么總有 。如果 是 S 上一個任意點, ,那么 可以表示成一個第二類正規化阿貝爾微分 ,有限個第三類正規 阿貝爾微分 以及第一類阿貝爾微分 的線性組合: 。
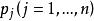 阿貝爾微分
阿貝爾微分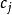 阿貝爾微分
阿貝爾微分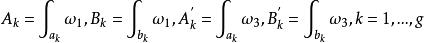 阿貝爾微分
阿貝爾微分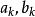 阿貝爾微分
阿貝爾微分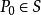 阿貝爾微分
阿貝爾微分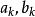 阿貝爾微分
阿貝爾微分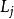 阿貝爾微分
阿貝爾微分 阿貝爾微分
阿貝爾微分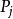 阿貝爾微分
阿貝爾微分設ω 是只在 有留數 的單極點的第三類 阿貝爾微分,ω是任意的一個第一類 阿貝爾微分: ,這裡的閉鏈 不通過ω 的極點。設 不在閉鏈 上, 是從 到 的一條道路。那么可得第一類和第三類 阿貝爾微分的雙線性關係(bilinear relation):
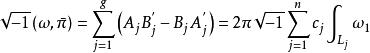 阿貝爾微分
阿貝爾微分在第一類和第二類 阿貝爾微分也有類似的雙線性關係。
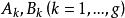 阿貝爾微分
阿貝爾微分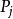 阿貝爾微分
阿貝爾微分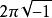 阿貝爾微分
阿貝爾微分 阿貝爾微分
阿貝爾微分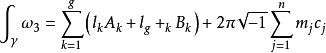 阿貝爾微分
阿貝爾微分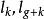 阿貝爾微分
阿貝爾微分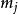 阿貝爾微分
阿貝爾微分除了被稱為循環周期 (cyclic period) 的 A 周期和 B 周期 外,一個任意的第三類阿貝尓微分還具有沿著圍繞 的零同調閉鏈的形如 的極周期 (polar period)。於是對任意的閉鏈 有 這裡 和 都是整數。
性質
阿貝爾微分的重要性質可以用除子描述。
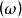 阿貝爾微分
阿貝爾微分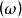 阿貝爾微分
阿貝爾微分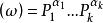 阿貝爾微分
阿貝爾微分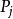 阿貝爾微分
阿貝爾微分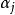 阿貝爾微分
阿貝爾微分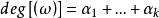 阿貝爾微分
阿貝爾微分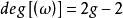 阿貝爾微分
阿貝爾微分 阿貝爾微分
阿貝爾微分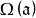 阿貝爾微分
阿貝爾微分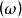 阿貝爾微分
阿貝爾微分 阿貝爾微分
阿貝爾微分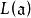 阿貝爾微分
阿貝爾微分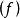 阿貝爾微分
阿貝爾微分 阿貝爾微分
阿貝爾微分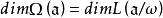 阿貝爾微分
阿貝爾微分設 是阿貝尓微分ω的除子,即 是一個形如 的表達式,其中 是ω的所有零點和極點, 是它們的重數或階數。 阿貝爾微分ω的除子的次數 僅依賴於 S 的虧格。且總有 。設 是某個已給的除子,用 表示簇子 是 的倍數的阿貝尓微分ω的復向量空間,用 表示其除子 是 的倍數的 S 上亞純函式 f 的向量空間,則 。關於這些空間的維數的另一重要信息包含在黎曼-羅赫定理中:等式
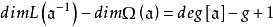 阿貝爾微分
阿貝爾微分 阿貝爾微分
阿貝爾微分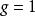 阿貝爾微分
阿貝爾微分對任意除子 成立。由上述可知,如當 ,即在環面上時,亞純函式不能有單獨的單極點。
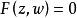 阿貝爾微分
阿貝爾微分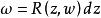 阿貝爾微分
阿貝爾微分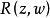 阿貝爾微分
阿貝爾微分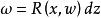 阿貝爾微分
阿貝爾微分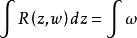 阿貝爾微分
阿貝爾微分設 S 是任意緊黎曼面,其上有滿足不可約代數方程 的亞純函式 z 和 ω,那么 S 上任意阿貝爾微分都可以表示成 ,其中 是 z 和 ω的一個有理函式;反之,表達式 是一個阿貝爾微分。這意味著任何阿貝爾積分 是緊黎曼面 S 上的某個 阿貝爾微分的積分。

