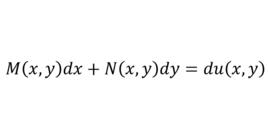定義
一階顯式方程
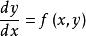 全微分方程
全微分方程 全微分方程
全微分方程 全微分方程
全微分方程可以改寫成關於 和 的對稱形式
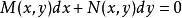 全微分方程
全微分方程(1)
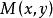 全微分方程
全微分方程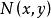 全微分方程
全微分方程 全微分方程
全微分方程 全微分方程
全微分方程這種形式有時便於求解。這裡 和 在某一矩形域 內是 的連續函式,且具有連續的一階偏導數。
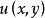 全微分方程
全微分方程如果存在一個二元函式 使得該方程的左端恰好是它的全微分,即有
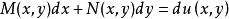 全微分方程
全微分方程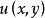 全微分方程
全微分方程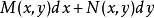 全微分方程
全微分方程則稱其為全微分方程(或恰當方程),而函式 是 的原函式。
全微分方程的通積分形式
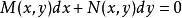 全微分方程
全微分方程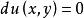 全微分方程
全微分方程當方程 是全微分方程時,它可寫成 ,於是其通積分就是
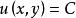 全微分方程
全微分方程(2)
 全微分方程
全微分方程其中 為任意常數。
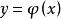 全微分方程
全微分方程事實上,設 是原方程的解,則有
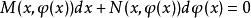 全微分方程
全微分方程即有
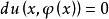 全微分方程
全微分方程 全微分方程
全微分方程對 積分得到
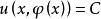 全微分方程
全微分方程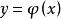 全微分方程
全微分方程這表明滿足方程(2)。
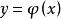 全微分方程
全微分方程反之,設是函式方程(2)的解,即它是由(2)所確定的隱函式,則有
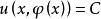 全微分方程
全微分方程 全微分方程
全微分方程對微分得到
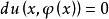 全微分方程
全微分方程即
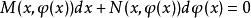 全微分方程
全微分方程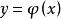 全微分方程
全微分方程這表明滿足方程(1)。
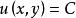 全微分方程
全微分方程因此全微分方程的通積分形式是。
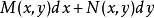 全微分方程
全微分方程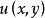 全微分方程
全微分方程根據上述表述,為了求解方程(1),只要求出的一個原函式,就可得到方程(1)的通積分(2)。
全微分方程的判別與求解
①如何判別方程(1)為全微分方程,這個問題在數學內早有結論,即
方程(1)是全微分方程的充分必要條件是
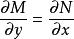 全微分方程
全微分方程 全微分方程
全微分方程在矩形域內成立。
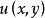 全微分方程
全微分方程②如果已判定方程(1)為全微分方程,如何求出相應全微分的原函式,這個問題在數學分析中也已經得到解決,最常用的方法是不定積分法。
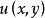 全微分方程
全微分方程因為所求的原函式適應方程組
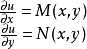 全微分方程
全微分方程 全微分方程
全微分方程 全微分方程
全微分方程首先由第一個式子出發,把看成參數,兩邊對積分,得
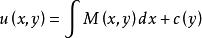 全微分方程
全微分方程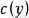 全微分方程
全微分方程 全微分方程
全微分方程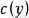 全微分方程
全微分方程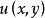 全微分方程
全微分方程其中是的任意可微函式,而且要選擇適當的,使滿足第二個式子。為此,將其代入第二個等式得
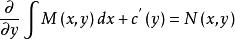 全微分方程
全微分方程即
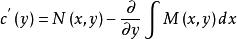 全微分方程
全微分方程 全微分方程
全微分方程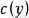 全微分方程
全微分方程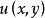 全微分方程
全微分方程兩邊對積分,即可得到,再代回之前的積分,即可得到。
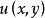 全微分方程
全微分方程但對於某些特殊的全微分方程,為了求出相應全微分的原函式,還可以採用相對簡單的“分組湊全微分”的方法,即把方程的左端各項進行重新組合,使每個組的原函式容易觀察得出,從而可以寫出。
而對於不是全微分的方程,可以採用積分因子使其成為全微分方程,再根據以上方法求解。