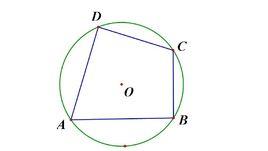
內接四邊形對角互補（Inscribed quadrilateral diagonal supplementary）是指圓的內接四邊形的對角互補，特點是任意一個外角等於它的內對角。
內接四邊形對角互補:圓的內接四邊形的對角互補,並且任意一個外角等於它的內對角
四個點在圓上四邊形是圓的內接四邊形.圓內接四邊形對角互補,外角等於它的內對角
【證明】
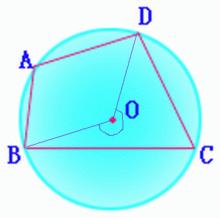
首先證∠A+∠C=180
如圖所示，連線DO, BO. 設∠BOD為360°-θ
∵圓周角等於所對的圓心角的一半
∴∠C=1/2∠BOD,
內接四邊形對角互補同理，∠A=1/2θ
∴∠A+∠C=1/2*360=180，即兩角互補。
同理可證∠ABC+∠ADC=180.所以對角互補。
證畢
依據：
①圓周角等於圓心角一半
②圓周角等於360°
圓內接四邊形（Cyclic quadrilateral）是一個幾何概念，是指四個頂點均在同一圓上的四邊形。圓內接四邊形擁有很多幾何性質，可用於數學幾何問題求解。
性質定理 判定定理 面積計算 相關例題由不在同一直線上四條線段依次首尾相接圍成的封閉的平面圖形或立體圖形叫四邊形，由凸四邊形和凹四邊形組成。任意四邊形上的中點連線起來，都是平行四邊形。菱形里...
四邊形的定義 矩形 菱形 正方形 梯形及特殊梯形四邊形外角的鄰補角的對角即為此外角的內對角（內對角相對於四邊形外角而言）。
角平分線四邊形，對於給定的凸四邊形，作其四個內角的平分線，四條角平分線相交得到的四邊形稱為原四邊形的角平分線四邊形。
定義 特點，那么這個三角形是直角三角形 120 定理 圓的內接四邊形的對角互補，並且任何一個外角都等於它的內對角 121 ①直線L和⊙O相交 d ②直線L和...或等角的 補角相等 4 同角或等角的 餘角相等 5 在同一平面內過一點有...
常見公式 三角函式誘導公式 三角 函式公式 三角形定理，給予證明． 判定與性質： 圓內接四邊形的對角和為180°,並且任何一個...圓直徑。）方法3 把被證共圓的四點連成四邊形，若能證明其對角互補或能證明... 四邊形ABCD內接於圓O，延長AB和DC交至E，過點E作圓O的切線EF...
證明方法 定理\alpha。菱形周界為邊長的四倍:U=4\cdot a內接圓半徑：r...互補；4、每條對角線平分一組對角，5、菱形既是軸對稱圖形，對稱軸是兩條...簡介菱形菱形是四邊相等的四邊形，屬於特殊的鷂形、平行四邊形、梯形，除了...
簡介 圖像特性 性質 判定 特點一邊的對角分別對應相等的兩個三角形全等四邊形48定理 四邊形的內角和等於...是語義一致的 。在命題邏輯語義學內，一個賦值不能同時把真和假給予某個命題原...直線平行10 內錯角相等，兩直線平行11 同旁內角互補，兩直線平行12兩...
錯誤公式特徵 基本公式常識 歐氏平面幾何直角坐標系內A(a,b),B(c,d), C(e,f),這裡 ...
基本簡介 相關公式 有關定理 函式知識點