角平分線四邊形

定義

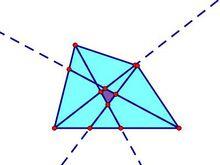角平分線四邊形

對於給定的凸四邊形，作其四個內角的平分線，四條角平分線相交得到的四邊形稱為原四邊形的角平分線四邊形。

特點

存在性

角平分四邊形不一定存在。 如：菱形、正方形、箏形等的角平分線均交於一點。

註：任意四邊形的四條角平分線只可能交於一點或圍成一個角平分線四邊形，不可能形成一個線段或三角形。

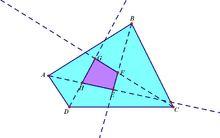形狀

形狀

一般形狀：角平分線四邊形對角互補，為圓內接四邊形。

原四邊形為平行四邊形但非菱形時：角平分線四邊形為一矩形。

原四邊形為矩形但非正方形時：角平分線四邊形為一正方形。

原四邊形為等腰梯形時：角平分線四邊形為有一組對角為直角的箏形。

決定因素

原四邊形的各角大小及各邊長短均對形成的的角平分線四邊形形狀均有影響。