定義
首先介紹無窮小量的概念。
 低階無窮小
低階無窮小 低階無窮小
低階無窮小 低階無窮小
低階無窮小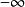 低階無窮小
低階無窮小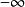 低階無窮小
低階無窮小初學者應當注意的是,無窮小量是極限為0的變數而不是數量0,是指自變數在一定變動方式下其極限為數量0,稱一個函式是無窮小量,一定要說明自變數的變化趨勢。例如在時是無窮小量,而不能籠統說是無窮小量。也不能說無窮小是,是指負無窮大。
設f在某x的空心鄰域有定義。
 低階無窮小
低階無窮小 低階無窮小
低階無窮小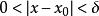 低階無窮小
低階無窮小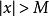 低階無窮小
低階無窮小 低階無窮小
低階無窮小 低階無窮小
低階無窮小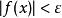 低階無窮小
低階無窮小 低階無窮小
低階無窮小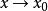 低階無窮小
低階無窮小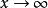 低階無窮小
低階無窮小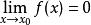 低階無窮小
低階無窮小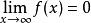 低階無窮小
低階無窮小對於任給的正數 ε(無論它多么小),總存在正數(或正數)使得不等式(或)的一切對應的函式值都滿足不等式,則稱函式為當(或)時的無窮小量。記做:(或)。
 低階無窮小
低階無窮小若,則稱“β 是比 α 較低階的無窮小”。意思是在某一過程中,β→0 比 α→0 慢一些。
 低階無窮小
低階無窮小例如,因為
所以 x→∞ 時,1/2x 是比 1/3x 較低階的無窮小。意思是在x→∞ 的過程中,1/2x→0 比1/3x →0 的速度慢。
無窮小的比較
觀察無窮小比值的極限:
 低階無窮小
低階無窮小兩個無窮小比值極限的各種不同情況,反映了不同的無窮小趨於零的“快慢”程度。在x→0 的過程中,x →0 比 3x→0 “快些”,反過來 3x→0 比 x →0 “慢些”,而 sin x→0 與 x→0 “快慢相仿”。
為了套用上的需要,我們就無窮小之比的極限存在或為無窮大時,給出下面的比較定義。
定義,設 α 及 β 都是同一個自變數的變化過程中的無窮小。
 低階無窮小
低階無窮小 低階無窮小
低階無窮小如果,就說β是比α高階的無窮小,記為;
 低階無窮小
低階無窮小如果,就說β是比α 低階的無窮小;
 低階無窮小
低階無窮小如果,就說β與α 是同階無窮小;
 低階無窮小
低階無窮小如果,就說β是關於 α 的k階無窮小;
 低階無窮小
低階無窮小如果,就說β與α 是等價無窮小,記為 β~α。

