簡介
交比亦稱非調和比。是分式線性變換的一種不變數。
在分式線性變換下任意四點的交比不變,換句話說,交比時線性變換的不變數。
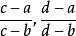 交比
交比設a,b,c,d是任意四個互異的有限複數,則稱為這四個數(或點)的交比,記為
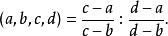 交比
交比推廣
交比的定義可推廣到a,b,c,d是無窮遠點的情況:給定四個有限點中的三個點,而令第四個點趨向於無窮遠點,則把四個交比在這一情形下的極限稱為四點中這一點是無窮遠點時的交比,即:
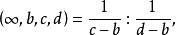 交比
交比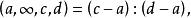 交比
交比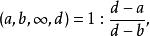 交比
交比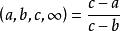 交比
交比發展
早在古希臘,數學家和天文學家就注意到這一比值的特性。
約公元100年,門內勞斯在《球面學》中用到了球面上的大圓弧相交的一個性質,類似於截線的交比不變性,用圓弧所對角的正弦比值來表示。
公元4世紀,帕波斯在《數學彙編》中明確闡述了一種交比的性質:設有四條線交於一點,則從一條線上的一點出發的截線所截點之間的交比相等。
到19世紀,施泰納、施陶特等數學家已將交比作為他們的射影幾何理論的基本工具,證明了四個共線點的交比在射影變換下不變的特性。
