定義
(1) 試驗中所有可能出現的基本事件只有有限個;
(2) 試驗中每個基本事件出現的可能性相等。
具有以上兩個特點的機率模型是大量存在的,這種機率模型稱為 古典機率模型,簡稱 古典概型,也叫 等可能概型。
特點
古典概型的特點
有限性(所有可能出現的基本事件只有有限個)
等可能性(每個基本事件出現的可能性相等)
基本事件的特點
(1)任何兩個基本事件是互斥的。
(2)任何事件(除不可能事件)都可以表示成基本事件的和。
古典概型的判斷
一個試驗是否為古典概型,在於這個試驗是否具有古典概型的兩個特徵——有限性和等可能性,只有同時具備這兩個特點的概型才是古典概型。
機率公式
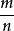 古典概型
古典概型P(A)==A包含的基本事件的個數m/基本事件的總數n
 古典概型
古典概型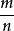 古典概型
古典概型如果一次實驗中可能出現的結果有n個,而且所有結果出現的可能性都相等,那么每一個基本事件的機率都是;如果某個事件A包含的結果有m個,那么事件A的機率為P(A)==A包含的基本事件的個數m/基本事件的總數n
基本步驟
 古典概型
古典概型(1)算出所有基本事件的個數n;
(2)求出事件A包含的所有基本事件數m;
(3)代入公式P(A)=m/n,求出P(A)。
模型的轉換
古典機率模型是在封閉系統內的模型,一旦系統內某個事件的機率在其他機率確定前被確定,其他事件機率也會跟著發生改變。機率模型會由古典概型轉變為幾何概型。
舉例
投擲一個質地均勻,形狀規範的硬幣,正面和反面出現的機率是一樣的,都是1/2。很多人會有問,為什麼正面和反面出現的機率是一樣的?顯然,硬幣是質地均勻,形狀規範的,哪一面都不會比另一面有更多的出現機會,正面和反面出現的機率是一樣的。這稱為古典概型的對稱性,體育比賽經常用到這個規律來決定誰開球,誰選場地。為了解釋這個現象,在歷史上,有很多大師對這個問題進行過驗證結果可以看出,隨著次數的不斷增加,正面出現的頻率越來越接近50%,我們也有理由相信,隨著次數的繼續增加,正面和反面出現的頻率將固定在1/2處,即正面和反面出現的機率都為1/2。
這是個典型的古典概型的例子,它的特點是:實驗結果只有有限個,而且每個實驗結果出現的機率是一樣的。正因為這兩個特點,我們能夠很容易算出來每個實驗結果出現的機率,應該是實驗結果個數的倒數。如上例中,實驗結果只有正面和反面,所以,正面和反面出現的機率為2的倒數1/2 。