伯努利試驗

伯努利試驗(Bernoulli experiment)是在同樣的條件下重複地、各次之間相互獨立地進行的一種試驗。一般地，在相同條件下重複做n次的試驗稱為n次獨立重複試驗。1. “在相同條件下”等價於各次試驗的結果不會受其他實驗結果的影響。2.如何判斷：判斷是否為伯努利試驗的關鍵是每次試驗事件A的機率不變，並且每次試驗的結果同其他各次試驗的結果無關，重複是指試驗為一系列的試驗，並非一次試驗，而是多次，但要注意重複事件發生的機率相互之間沒有影響。

定義與特徵

一般地，在相同條件下重複做n次的試驗稱為n次獨立重複試驗。

1. “在相同條件下”等價於各次試驗的結果不會受其他實驗結果的影響。

2.如何判斷：判斷是否為伯努利試驗的關鍵是每次試驗事件A的機率不變，並且每次試驗的結果同其他各次試驗的結果無關，重複是指試驗為一系列的試驗，並非一次試驗，而是多次，但要注意重複事件發生的機率相互之間沒有影響。

二項分布

一般地，在n次獨立重複試驗中，用ξ表示事件A發生的次數，如果事件發生的機率是P,則不發生的機率

q=1-p，

N次獨立重複試驗中發生K次的機率是

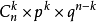伯努利試驗

P(ξ=K)=

(K=1,2,3,…n）

那么就說ξ服從二項分布。.其中P稱為成功機率。

記作：ξ~B(n,p)

期望：Eξ=np

方差：Dξ=npq

幾何分布

在第n次伯努利試驗中，試驗k次才得到第一次成功的機率。詳細的說是：前k-1次皆失敗，第k次成功的機率。

如果事件發生的機率是P,則不發生的機率q=1-p，則

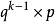伯努利試驗

P(ξ=K) =

具有這種分布列的隨機變數，稱為服從參數p的幾何分布。

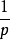伯努利試驗

幾何分布的期望EX=

，方差DX=

.