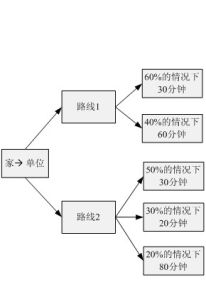
原理
 決策樹
決策樹決策樹提供了一種展示類似在什麼條件下會得到什麼值這類規則的方法。比如,在貸款申請中,要對申請的風險大小做出判斷,圖是為了解決這個問題而建立的一棵決策樹,從中我們可以看到決策樹的基本組成部分:決策節點、分支和葉子。決策樹中最上面的節點稱為根節點,是整個決策樹的開始。
本例中根節點是“收入>¥40,000”,對此問題的不同回答產生了“是”和“否”兩個分支。決策樹的每個節點子節點的個數與決策樹在用的算法有關。如CART算法得到的決策樹每個節點有兩個分支,這種樹稱為二叉樹。允許節點含有多於兩個子節點的樹稱為多叉樹。決策樹的內部節點(非樹葉節點)表示在一個屬性上的測試。每個分支要么是一個新的決策節點,要么是樹的結尾,稱為葉子。在沿著決策樹從上到下遍歷的過程中,在每個節點都會遇到一個問題,對每個節點上問題的不同回答導致不同的分支,最後會到達一個葉子節點。這個過程就是利用決策樹進行分類的過程,利用幾個變數(每個變數對應一個問題)來判斷所屬的類別(最後每個葉子會對應一個類別)。套用
假如負責借貸的銀行官員利用上面這棵決策樹來決定支持哪些貸款和拒絕哪些貸款,那么他就可以用貸款申請表來運行這棵決策樹,用決策樹來判斷風險的大小。“年收入>¥40,00”和“高負債”的用戶被認為是“高風險”,同時“收入<¥40,000”但“工作時間>5年”的申請,則被認為“低風險”而建議貸款給他/她。數據挖掘中決策樹是一種經常要用到的技術,可以用於分析數據,同樣也可以用來作預測(就像上面的銀行官員用他來預測貸款風險)。常用的算法有CHAID、CART、Quest和C5.0。建立決策樹的過程,即樹的生長過程是不斷的把數據進行切分的過程,每次切分對應一個問題,也對應著一個節點。對每個切分都要求分成的組之間的“差異”最大。區別
各種決策樹算法之間的主要區別就是對這個“差異”衡量方式的區別。對具體衡量方式算法的討論超出了本文的範圍,在此我們只需要把切分看成是把一組數據分成幾份,份與份之間儘量不同,而同一份內的數據儘量相同。這個切分的過程也可稱為數據的“純化”。看我們的例子,包含兩個類別--低風險和高風險。如果經過一次切分後得到的分組,每個分組中的數據都屬於同一個類別,顯然達到這樣效果的切分方法就是我們所追求的。到現在為止我們所討論的例子都是非常簡單的,樹也容易理解,當然實際中套用的決策樹可能非常複雜。假定我們利用歷史數據建立了一個包含幾百個屬性、輸出的類有十幾種的決策樹,這樣的一棵樹對人來說可能太複雜了,但每一條從根結點到葉子節點的路徑所描述的含義仍然是可以理解的。決策樹的這種易理解性對數據挖掘的使用者來說是一個顯著的優點。缺點
然而決策樹的這種明確性可能帶來誤導。比如,決策樹每個節點對應分割的定義都是非常明確毫不含糊的,但在實際生活中這種明確可能帶來麻煩(憑什麼說年收入¥40,001的人具有較小的信用風險而¥40,000的人就沒有)。建立一顆決策樹可能只要對資料庫進行幾遍掃描之後就能完成,這也意味著需要的計算資源較少,而且可以很容易的處理包含很多預測變數的情況,因此決策樹模型可以建立得很快,並適合套用到大量的數據上。對最終要拿給人看的決策樹來說,在建立過程中讓其生長的太“枝繁葉茂”是沒有必要的,這樣既降低了樹的可理解性和可用性,同時也使決策樹本身對歷史數據的依賴性增大,也就是說這是這棵決策樹對此歷史數據可能非常準確,一旦套用到新的數據時準確性卻急劇下降,我們稱這種情況為訓練過度。為了使得到的決策樹所蘊含的規則具有普遍意義,必須防止訓練過度,同時也減少了訓練的時間。因此我們需要有一種方法能讓我們在適當的時候停止樹的生長。常用的方法是設定決策樹的最大高度(層數)來限制樹的生長。還有一種方法是設定每個節點必須包含的最少記錄數,當節點中記錄的個數小於這個數值時就停止分割。與設定停止增長條件相對應的是在樹建立好之後對其進行修剪。先允許樹儘量生長,然後再把樹修剪到較小的尺寸,當然在修剪的同時要求儘量保持決策樹的準確度儘量不要下降太多。評論
對決策樹常見的批評是說其在為一個節點選擇怎樣進行分割時使用“貪心”算法。此種算法在決定當前這個分割時根本不考慮此次選擇會對將來的分割造成什麼樣的影響。換句話說,所有的分割都是順序完成的,一個節點完成分割之後不可能以後再有機會回過頭來再考察此次分割的合理性,每次分割都是依賴於他前面的分割方法,也就是說決策樹中所有的分割都受根結點的第一次分割的影響,只要第一次分割有一點點不同,那么由此得到的整個決策樹就會完全不同。那么是否在選擇一個節點的分割的同時向後考慮兩層甚至更多的方法,會具有更好的結果呢?目前我們知道的還不是很清楚,但至少這種方法使建立決策樹的計算量成倍的增長,因此現在還沒有哪個產品使用這種方法。而且,通常的分割算法在決定怎么在一個節點進行分割時,都只考察一個預測變數,即節點用於分割的問題只與一個變數有關。這樣生成的決策樹在有些本應很明確的情況下可能變得複雜而且意義含混,為此目前新提出的一些算法開始在一個節點同時用多個變數來決定分割的方法。比如以前的決策樹中可能只能出現類似“收入<¥35,000”的判斷,現在則可以用“收入<(0.35*抵押)”或“收入>¥35,000或抵押<150,000”這樣的問題。
優勢
決策樹很擅長處理非數值型數據,這與神經網路只能處理數值型數據比起來,就免去了很多數據預處理工作。甚至有些決策樹算法專為處理非數值型數據而設計,因此當採用此種方法建立決策樹同時又要處理數值型數據時,反而要做把數值型數據映射到非數值型數據的預處理。分析法
決策樹分析法是通過決策樹圖形展示臨床重要結局,明確思路,比較各種備選方案預期結果進行決策的方法。決策樹分析法通常有6個步驟。
第一步:明確決策問題,確定備選方案。對要解決的問題應該有清楚的界定,應該列出所有可能的備選方案。
第二步:繪出決策樹圖形。決策樹用3種不同的符號分別表示決策結、機會結、結局結。決策結用圖形符號如方框表示,放在決策樹的左端,每個備選方案用從該結引出的]個臂(線條)表示;實施每一個備選方案時都司能發生一系列受機遇控制的機會事件,用圖形符號圓圈表示,稱為機會結,每一個機會結司以有多個直接結局,例如某種治療方案有3個結局(治癒、改善、藥物毒性致死),則機會結有3個臂。最終結局用圖形符號如小三角形表示,稱為結局結,總是放在決策樹最右端。從左至右機會結的順序應該依照事件的時間先後關係而定。但不管機會結有多少個結局,從每個機會結引出的結局必須是互相排斥的狀態,不能互相包容或交叉。
第三步:明確各種結局可能出現的機率。可以從文獻中類似的病人去查找相關的機率,也可以從臨床經驗進行推測。所有這些機率都要在決策樹上標示出來。在為每一個機會結髮出的直接結局臂標記發生機率時,必須注意各機率相加之和必須為1.0。
第四步:對最終結局用適宜的效用值賦值。效用值是病人對健康狀態偏好程度的測量,通常套用0-1的數字表示,一般最好的健康狀態為1,死亡為0。有時可以用壽命年、質量調整壽命年表示。
第五步:計算每一種備遠方案的期望值。計算期望值的方法是從"樹尖"開始向"樹根"的方向進行計算,將每一個機會結所有的結局效用值與其發生機率分別相乘,其總和為該機會結的期望效用值。在每一個決策臂中,各機會結的期望效用值分別與其發生機率相乘,其總和為該決策方案的期望效用值,選擇期望值最高的備選方案為決策方案。
第六步:套用敏感性試驗對決策分析的結論進行測試。敏感分析的目的是測試決策分析結論的真實性。敏感分析要回答的問題是當機率及結局效用值等在一個合理的範圍內變動時,決策分析的結論會不會改變。
畫法
機器學習中,決策樹是一個預測模型;他代表的是對象屬性與對象值之間的一種映射關係。樹中每個節點表示某個對象,而每個分叉路徑則代表的某個可能的屬性值,而每個葉結點則對應從根節點到該葉節點所經歷的路徑所表示的對象的值。決策樹僅有單一輸出,若欲有複數輸出,可以建立獨立的決策樹以處理不同輸出。數據挖掘中決策樹是一種經常要用到的技術,可以用於分析數據,同樣也可以用來作預測。從數據產生決策樹的機器學習技術叫做決策樹學習,通俗說就是決策樹。
一個決策樹包含三種類型的節點:
決策節點:通常用矩形框來表式
機會節點:通常用圓圈來表式
終結點:通常用三角形來表示
決策樹學習也是資料探勘中一個普通的方法。在這裡,每個決策樹都表述了一種樹型結構,它由它的分支來對該類型的對象依靠屬性進行分類。每個決策樹可以依靠對源資料庫的分割進行數據測試。這個過程可以遞歸式的對樹進行修剪。當不能再進行分割或一個單獨的類可以被套用於某一分支時,遞歸過程就完成了。另外,隨機森林分類器將許多決策樹結合起來以提升分類的正確率。
決策樹同時也可以依靠計算條件機率來構造。
決策樹如果依靠數學的計算方法可以取得更加理想的效果。資料庫已如下所示:
(x,y)=(x1,x2,x3…,xk,y)
相關的變數Y表示我們嘗試去理解,分類或者更一般化的結果。其他的變數x1,x2,x3等則是幫助我們達到目的的變數。
實例
為了適應市場的需要,某地準備擴大電視機生產。市場預測表明:產品銷路好的機率為0.7;銷路差的機率為0.3。備選方案有三個:第一個方案是建設大工廠,需要投資600萬元,可使用10年;如銷路好,每年可贏利200萬元;如銷路不好,每年會虧損40萬元。第二個方案是建設小工廠,需投資280萬元;如銷路好,每年可贏利80萬元;如銷路不好,每年也會贏利60萬元。第三個方案也是先建設小工廠,但是如銷路好,3年後擴建,擴建需投資400萬元,可使用7年,擴建後每年會贏利190萬元。各點期望:點②:0.7×200×10+0.3×(-40)×10-600(投資)=680(萬元)
決策樹分析
點⑤:1.0×190×7-400=930(萬元)
點⑥:1.0×80×7=560(萬元)
比較決策點4的情況可以看到,由於點⑤(930萬元)與點⑥(560萬元)相比,點⑤的期望利潤值較大,因此應採用擴建的方案,而捨棄不擴建的方案。把點⑤的930萬元移到點4來,可計算出點③的期望利潤值。
點③:0.7×80×3+0.7×930+0.3×60×(3+7)-280 = 719(萬元)
最後比較決策點1的情況。由於點③(719萬元)與點②(680萬元)相比,點③的期望利潤值較大,因此取點③而舍點②。這樣,相比之下,建設大工廠的方案不是最優方案,合理的策略應採用前3年建小工廠,如銷路好,後7年進行擴建的方案。